Figure 7 shows a circuit designed by a student to monitor temperature changes. The supply has negligible internal resistance and the thermistor has a resistance of 750 Ω at room temperature. The student wants the output potential difference (pd) at room temperature to be 5.0 V. The 0.25 kΩ resistor is made of 50 turns of wire that is wound around a non-conducting cylinder of diameter 8.0 mm. Resistivity of the wire = 4.2 × 10^−7 Ω m Determine the area of cross-section of the wire that has been used for the resistor. The student selects a resistor rated at 0.36 W for the 0.25 kΩ resistor in Figure 7. Determine whether this resistor is suitable. Determine the value of R that the student should select. Give your answer to an appropriate number of significant figures. State and explain the effect on the output pd of increasing the temperature of the thermistor.

Photo AI

Figure 7 shows a circuit designed by a student to monitor temperature changes - AQA - A-Level Physics - Question 4 - 2018 - Paper 1

Question 4

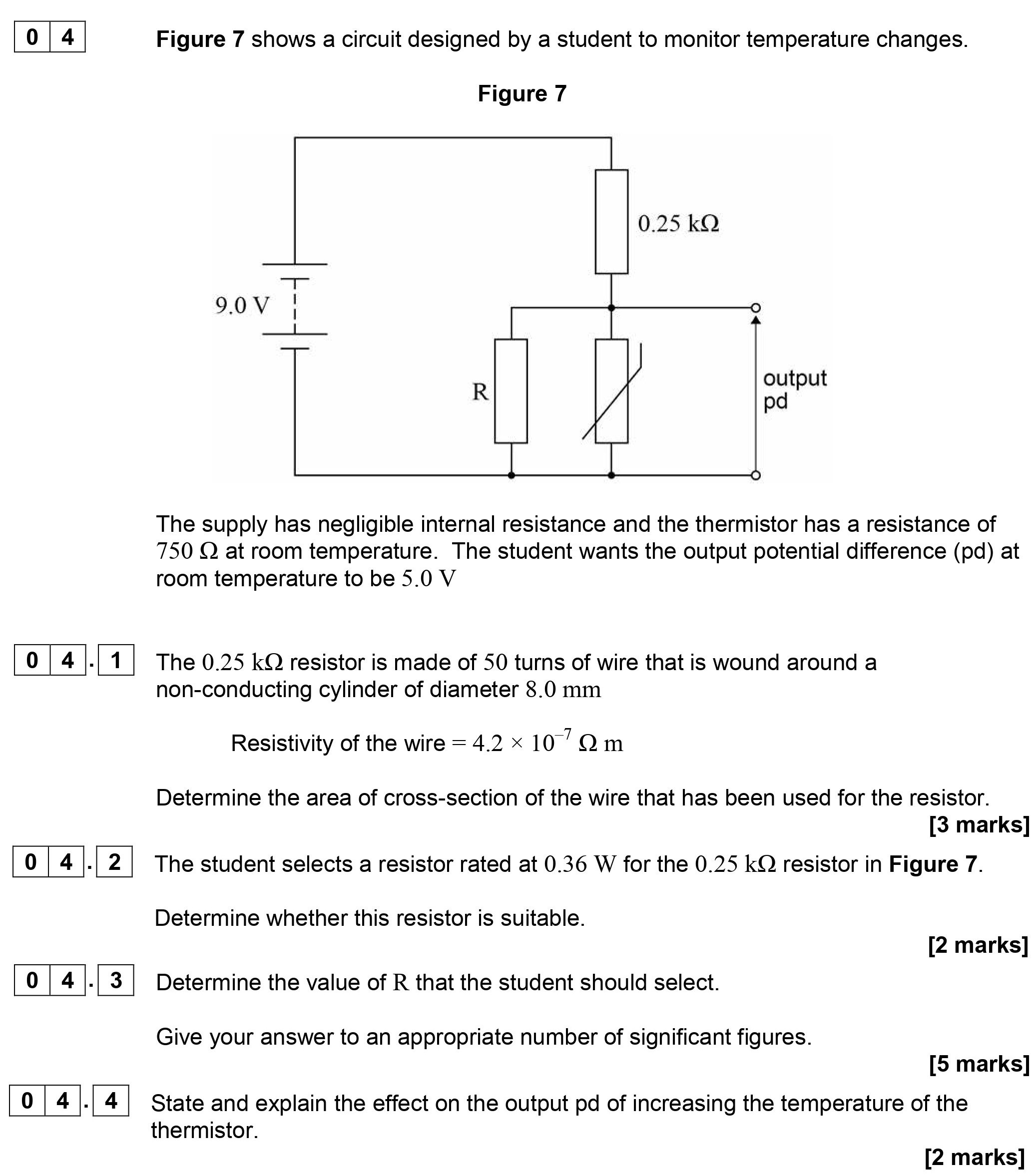
Figure 7 shows a circuit designed by a student to monitor temperature changes. The supply has negligible internal resistance and the thermistor has a resistance of ... show full transcript

Worked Solution & Example Answer:Figure 7 shows a circuit designed by a student to monitor temperature changes - AQA - A-Level Physics - Question 4 - 2018 - Paper 1

Step 1

Determine the area of cross-section of the wire that has been used for the resistor.

96%

114 rated

Answer

To determine the area of cross-section (A) of the wire, we utilize the formula for resistance:

$R = \rho \frac{L}{A}$

Where:

$R$ is the resistance (0.25 kΩ = 250 Ω)
$\rho$ is the resistivity of the wire ( $4.2 × 10^{-7} Ω m$ )
$L$ is the length of the wire

First, we find the diameter of the cylindrical wire: $\text{Diameter} = 8.0 \text{ mm} = 0.008 \text{ m}$

To find the circumference: $C = \pi \times ext{Diameter} = \pi \times 0.008 ext{ m} \approx 0.0251 ext{ m}$

Total length for 50 turns: $L = 50 \times C = 50 \times 0.0251 ext{ m} \approx 1.255 ext{ m}$

Rearranging the formula for area gives: $A = \frac{\rho \times L}{R} = \frac{(4.2 × 10^{-7} Ω m) \times (1.255 m)}{250 Ω} \approx 2.1 × 10^{-9} m^2$

Step 2

Determine whether this resistor is suitable.

99%

104 rated

Answer

To assess the suitability, we calculate the maximum power for the 0.25 kΩ resistor, which is determined by:

$P_{max} = \frac{V^2}{R}$

Where $V = 9.5 V$ is the supply voltage:

$P_{max} = \frac{(9.5^2)}{250} = \frac{90.25}{250} = 0.361 W$

Since the rated power of the selected resistor is 0.36 W, it is approximately equal to the maximum power dissipation.

Thus, this resistor is deemed suitable as it can safely handle the power without exceeding its limits.

Step 3

Determine the value of R that the student should select.

96%

101 rated

Answer

Using the potential divider equation to find the value of resistance R:

Given that the desired output potential difference (pd) is 5.0 V,

We apply the equation:

$V_{out} = V_{in} \times \frac{R}{R + R_{thermistor}}$

Where:

$V_{in} = 9.0 V$
$R_{thermistor} = 750 Ω$
$V_{out} = 5.0 V$

Rearranging the equation gives:

$5 = 9 \times \frac{R}{R + 750}$

Cross-multiplying to find R:

i 5R + 3750 = 9R$$

Solving yields:

ightarrow R = \frac{3750}{4} = 937.5 Ω$$

Step 4

Give your answer to an appropriate number of significant figures.

98%

120 rated

Answer

The value of R determined is 937.5 Ω, which can be correctly rounded to three significant figures as: 938 Ω.

Step 5

State and explain the effect on the output pd of increasing the temperature of the thermistor.

97%

117 rated

Answer

As the temperature of the thermistor increases, its resistance decreases.

In a potential divider circuit, lowering the resistance of the thermistor will result in a higher proportion of the input voltage being dropped across the resistor R.

This leads to an increase in the output pd. Therefore, an increase in temperature will yield a higher output voltage from the circuit, affecting the intended measurements of the temperature changes monitored.

Figure 7 shows a circuit designed by a student to monitor temperature changes - AQA - A-Level Physics - Question 4 - 2018 - Paper 1

Worked Solution & Example Answer:Figure 7 shows a circuit designed by a student to monitor temperature changes - AQA - A-Level Physics - Question 4 - 2018 - Paper 1

Determine the area of cross-section of the wire that has been used for the resistor.

Determine whether this resistor is suitable.

Determine the value of R that the student should select.

Give your answer to an appropriate number of significant figures.

State and explain the effect on the output pd of increasing the temperature of the thermistor.

Join the A-Level students using SimpleStudy...