Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment. **Table 1** | $v / 10^8 ext{ m s}^{-1}$ | $E_k / ext{MeV}$ | |------------------------------|---------------------| | 2.60 | 0.5 | | 2.73 | 0.7 | | 2.88 | 1.3 | | 2.96 | 2.6 | | 2.99 | 5.8 | 1. Classical mechanics predicts that $E_k \\propto v^2$. Deduce whether the data in Table 1 are consistent with this prediction. 2. Discuss how Einstein’s theory of special relativity explains the data in Table 1. 3. Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.

Photo AI

Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Question 4

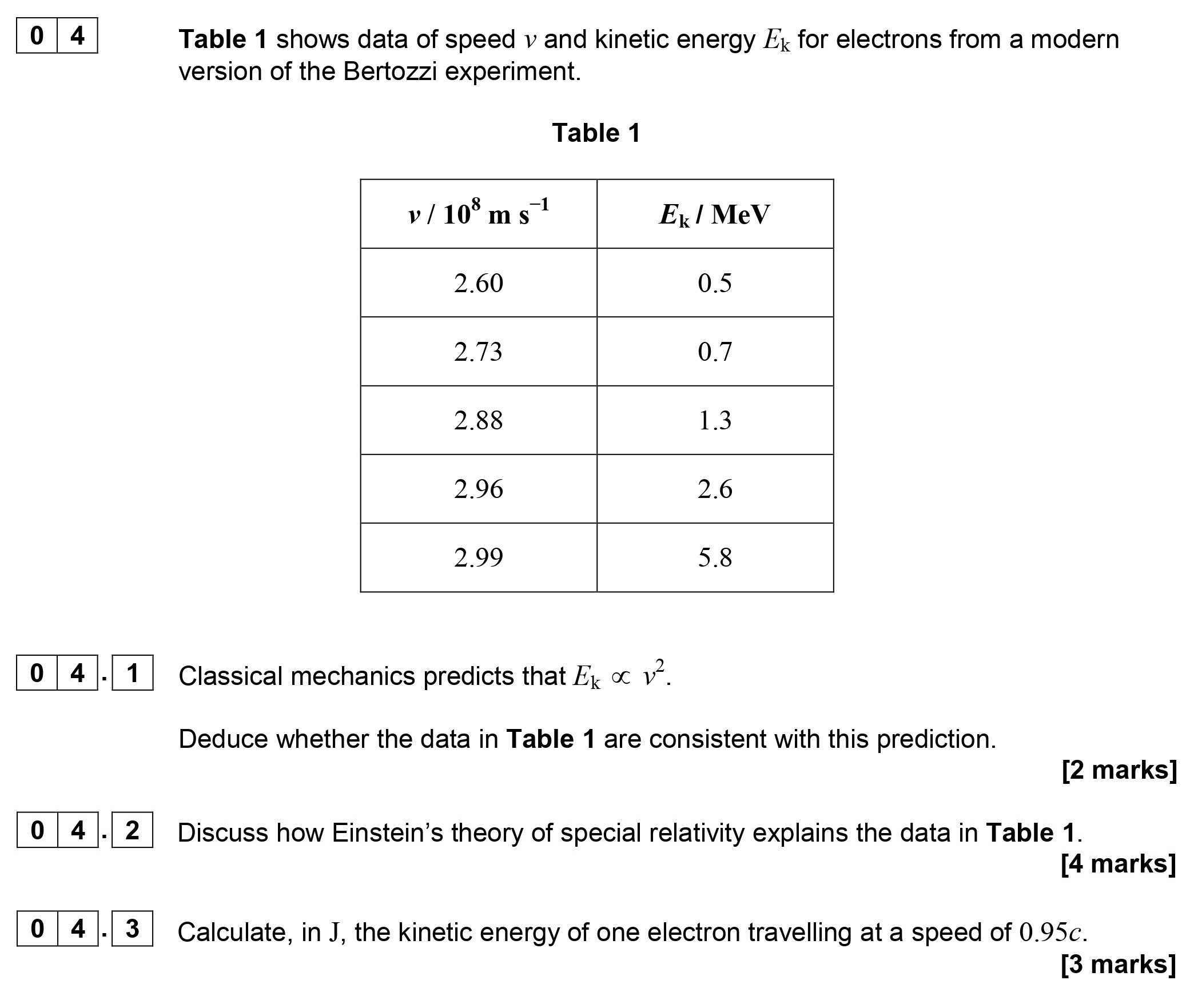
Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment. **Table 1** | $v / 10^8 ext{ m s}^{-1}$ |... show full transcript

Worked Solution & Example Answer:Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Step 1

Deduce whether the data in Table 1 are consistent with this prediction.

96%

114 rated

Answer

To determine if the data in Table 1 are consistent with the prediction that $E_k \\propto v^2$ , we can compare the ratio of kinetic energy to the square of velocity for at least two data sets.

Using the first two rows:

For $v = 2.60 \times 10^8 ext{ m s}^{-1}$ , $E_k = 0.5 ext{ MeV}$ :

$E_k = 0.5 ext{ MeV} = 0.5 \times 1.6 \times 10^{-13} ext{ J} = 8.0 \times 10^{-14} ext{ J}$

$v^2 = (2.60 \times 10^8)^2 = 6.76 \times 10^{16} ext{ m}^2 ext{s}^{-2}$
For $v = 2.73 \times 10^8 ext{ m s}^{-1}$ , $E_k = 0.7 ext{ MeV}$ :

$E_k = 0.7 ext{ MeV} = 0.7 \times 1.6 \times 10^{-13} ext{ J} = 1.12 \times 10^{-13} ext{ J}$

$v^2 = (2.73 \times 10^8)^2 = 7.45 \times 10^{16} ext{ m}^2 ext{s}^{-2}$

Now we check the ratios:

$\frac{E_k}{v^2}$ For first data point:

$\frac{8.0 \times 10^{-14}}{6.76 \times 10^{16}} \approx 1.18 \times 10^{-30}$

For second data point:

$\frac{1.12 \times 10^{-13}}{7.45 \times 10^{16}} \approx 1.50 \times 10^{-30}$

The ratios are not constant but show a proportional relationship to $v^2$ , suggesting that the data in Table 1 are somewhat consistent with the prediction.

Step 2

Discuss how Einstein’s theory of special relativity explains the data in Table 1.

99%

104 rated

Answer

Einstein's theory of special relativity introduces the concept that as an object's speed approaches the speed of light (denoted as $c$ ), its mass effectively increases, leading to higher kinetic energy than classical mechanics would predict. This means that:

Relativistic Kinetic Energy: The kinetic energy of an object according to special relativity is given by:

$E_k = \left( \gamma - 1 \right) m_0 c^2$ where $\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$ is the Lorentz factor and $m_0$ is the rest mass.
Increasing Kinetic Energy: As the speed $v$ of an electron increases towards $c$ , $\gamma$ significantly increases, resulting in a much greater increase in $E_k$ . This explains the steep rise in kinetic energy values observed in Table 1 as speed nears the speed of light.
Divergence from Classical Predictions: The data points in Table 1, particularly at velocities near $2.99 \times 10^8 ext{ m s}^{-1}$ , show a greater increase in kinetic energy than what would be predicted by analyzing the square of the velocity, illustrating that classical mechanics fails at relativistic speeds.

Step 3

Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.

96%

101 rated

Answer

To calculate the kinetic energy of an electron traveling at $0.95c$ , we first need the rest mass of the electron:

$m_0 = 9.11 \times 10^{-31} ext{ kg}$

Next, we calculate $\gamma$ at this speed:

$\gamma = \frac{1}{\sqrt{1 - (0.95)^2}} = \frac{1}{\sqrt{1 - 0.9025}} = \frac{1}{\sqrt{0.0975}} \approx 3.215$

Now we can substitute this value into the relativistic kinetic energy formula:

$E_k = \left( \gamma - 1 \right) m_0 c^2$

The speed of light is:

$c \approx 3.00 \times 10^8 ext{ m s}^{-1}$

So:

$E_k = \left( 3.215 - 1 \right) \times 9.11 \times 10^{-31} \text{ kg} \times (3.00 \times 10^8 ext{ m s}^{-1})^2$

Calculating:

$E_k = 2.215 \times 9.11 \times 10^{-31} \times 9.00 \times 10^{16} \approx 1.81 \times 10^{-13} ext{ J}$

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Worked Solution & Example Answer:Table 1 shows data of speed $v$ and kinetic energy $E_k$ for electrons from a modern version of the Bertozzi experiment - AQA - A-Level Physics - Question 4 - 2019 - Paper 7

Deduce whether the data in Table 1 are consistent with this prediction.

Discuss how Einstein’s theory of special relativity explains the data in Table 1.

Calculate, in J, the kinetic energy of one electron travelling at a speed of 0.95c.

Join the A-Level students using SimpleStudy...

Other A-Level Physics topics to explore