Photo AI
Using the data in the network diagram above, calculate the Earliest Start Time (EST) and Latest Finishing Times (LFT) for each activity and identify the critical path. - Edexcel - A-Level Business - Question 2 - 2017 - Paper 2
Question 2
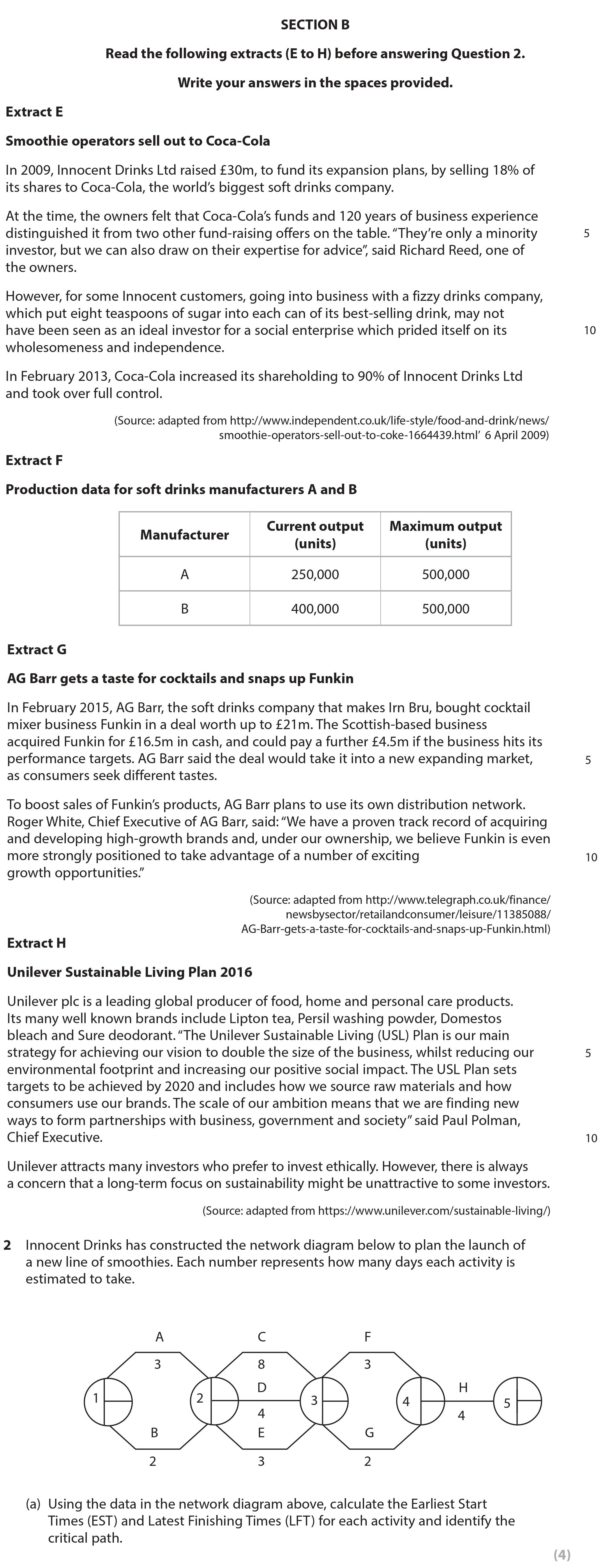
Using the data in the network diagram above, calculate the Earliest Start Time (EST) and Latest Finishing Times (LFT) for each activity and identify the critical pat... show full transcript
Worked Solution & Example Answer:Using the data in the network diagram above, calculate the Earliest Start Time (EST) and Latest Finishing Times (LFT) for each activity and identify the critical path. - Edexcel - A-Level Business - Question 2 - 2017 - Paper 2
Step 1
Calculate Earliest Start Time (EST)
Answer
- For activity A, since it has no dependencies, the EST is 0.
- For activity B, it can only start after A, so the EST for B is 0 + duration of A (0) = 0.
- Activity C can start after A, with the same calculation as B, thus, EST for C is also 0.
- For activity D, the EST is dependent on both B and C. As both have an EST of 0, the EST for D is 0 + duration of B (3) = 3.
- Activity E can start after D, so EST for E is 3 + duration of D (11) = 14.
- For activity F, it can only start after D, hence, EST for F is 3.
- Lastly, activity H can start just after F, giving it an EST of 14 + duration of F (18) = 32.
Step 2
Calculate Latest Finishing Time (LFT)
Answer
- For the last activity (H), LFT can be assumed as the EST of 32.
- Thus, for activity F, its LFT = LFT (H) - duration of H. If H takes 5 units, LFT for F becomes 32 - 5 = 27.
- For activity E, it must be completed before F starts, hence LFT for E is LFT (F) - duration of F (14). So LFT for E = 27 - 14 = 13.
- For D, since both E and F are dependent, we take the minimum of their LFTs. LFT for D = min(13, 27) = 13.
- For B, the LFT is determined by D, so LFT for B = LFT (D) - duration of B (3) = 10.
- Activity A's LFT is the minimum of B’s and C´s LFT, thus, LFT for A = min(10, 10) = 10.
- All calculations yield the following results:
- EST: A: 0, B: 0, C: 0, D: 3, E: 14, F: 3, H: 32
- LFT: A: 10, B: 10, C: 10, D: 13, E: 13, F: 27, H: 32
Step 3
