Photo AI
Charlie is studying the time it takes members of his company to travel to the office - Edexcel - A-Level Maths Mechanics - Question 4 - 2018 - Paper 1
Question 4
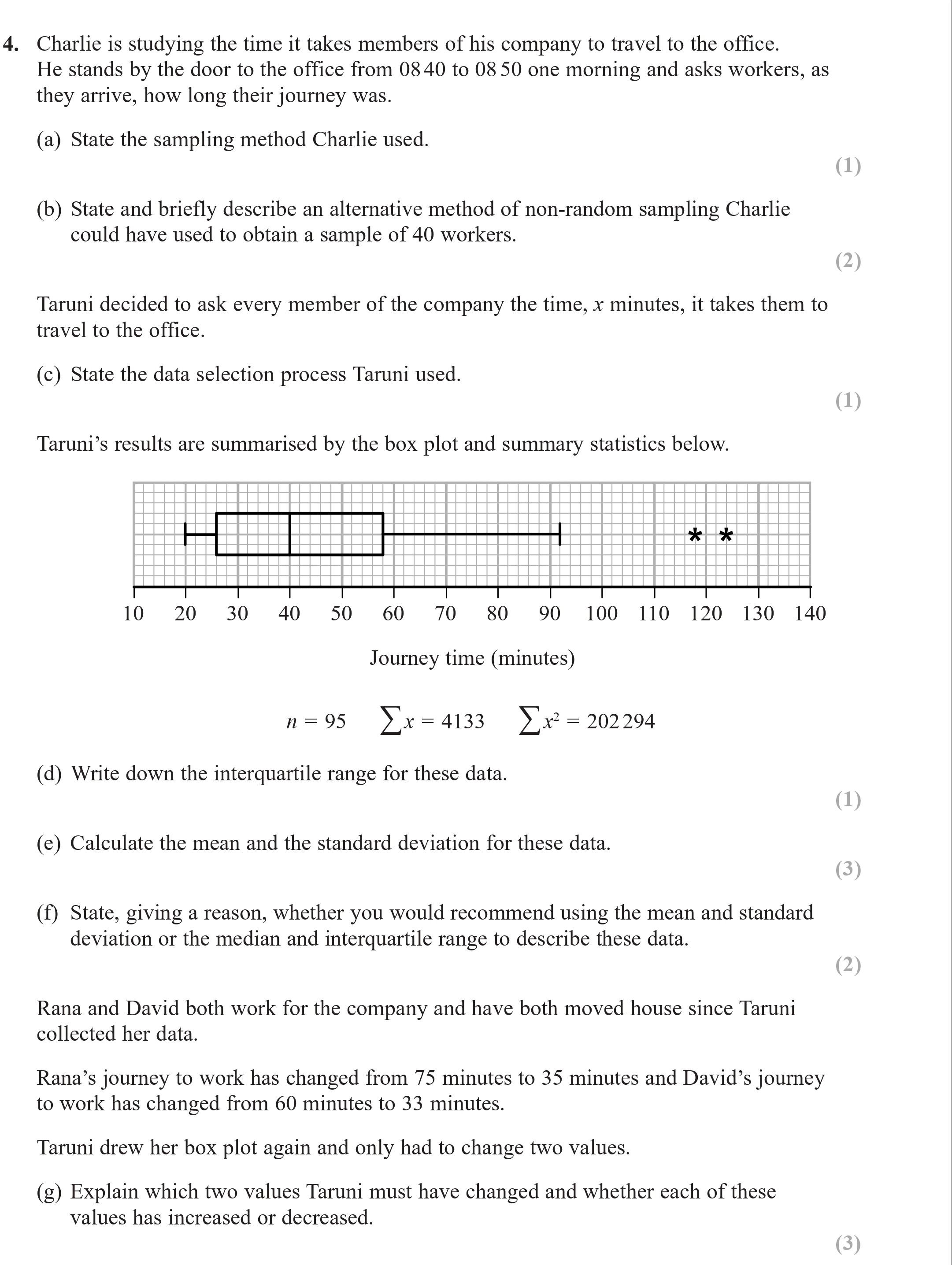
Charlie is studying the time it takes members of his company to travel to the office. He stands by the door to the office from 08:40 to 08:50 one morning and asks wo... show full transcript
Worked Solution & Example Answer:Charlie is studying the time it takes members of his company to travel to the office - Edexcel - A-Level Maths Mechanics - Question 4 - 2018 - Paper 1
Step 1
Step 2
State and briefly describe an alternative method of non-random sampling Charlie could have used to obtain a sample of 40 workers.
Answer
An alternative method could be quota sampling. For example, Charlie could decide to sample 10 workers from each department in the company, ensuring that he collects data from a variety of groups within the workforce.
Step 3
Step 4
Write down the interquartile range for these data.
Answer
To find the interquartile range (IQR), we calculate it as the difference between the upper quartile (Q3) and the lower quartile (Q1). Assuming the data summary and box plot indicate Q1 = 26 and Q3 = 40, the IQR can be calculated as follows:
Step 5
Step 6
State, giving a reason, whether you would recommend using the mean and standard deviation or the median and interquartile range to describe the data.
Answer
Given the presence of outliers in the data, it is recommended to use the median and interquartile range (IQR) rather than the mean and standard deviation. Outliers can skew the mean and inflate the standard deviation, making them less representative of the central tendency and spread of the data.
Step 7
Explain which two values Taruni must have changed and whether each of these values has increased or decreased.
Answer
The two values that Taruni must have changed are the mean and the standard deviation. The mean has likely decreased due to Rana's and David's reduced travel times, and the standard deviation would also decrease because the overall spread of the data would reduce with these lower values in the dataset.
