Photo AI

A non-uniform beam AD has weight W newtons and length 4 m - Edexcel - A-Level Maths Mechanics - Question 6 - 2014 - Paper 1

Question icon

Question 6

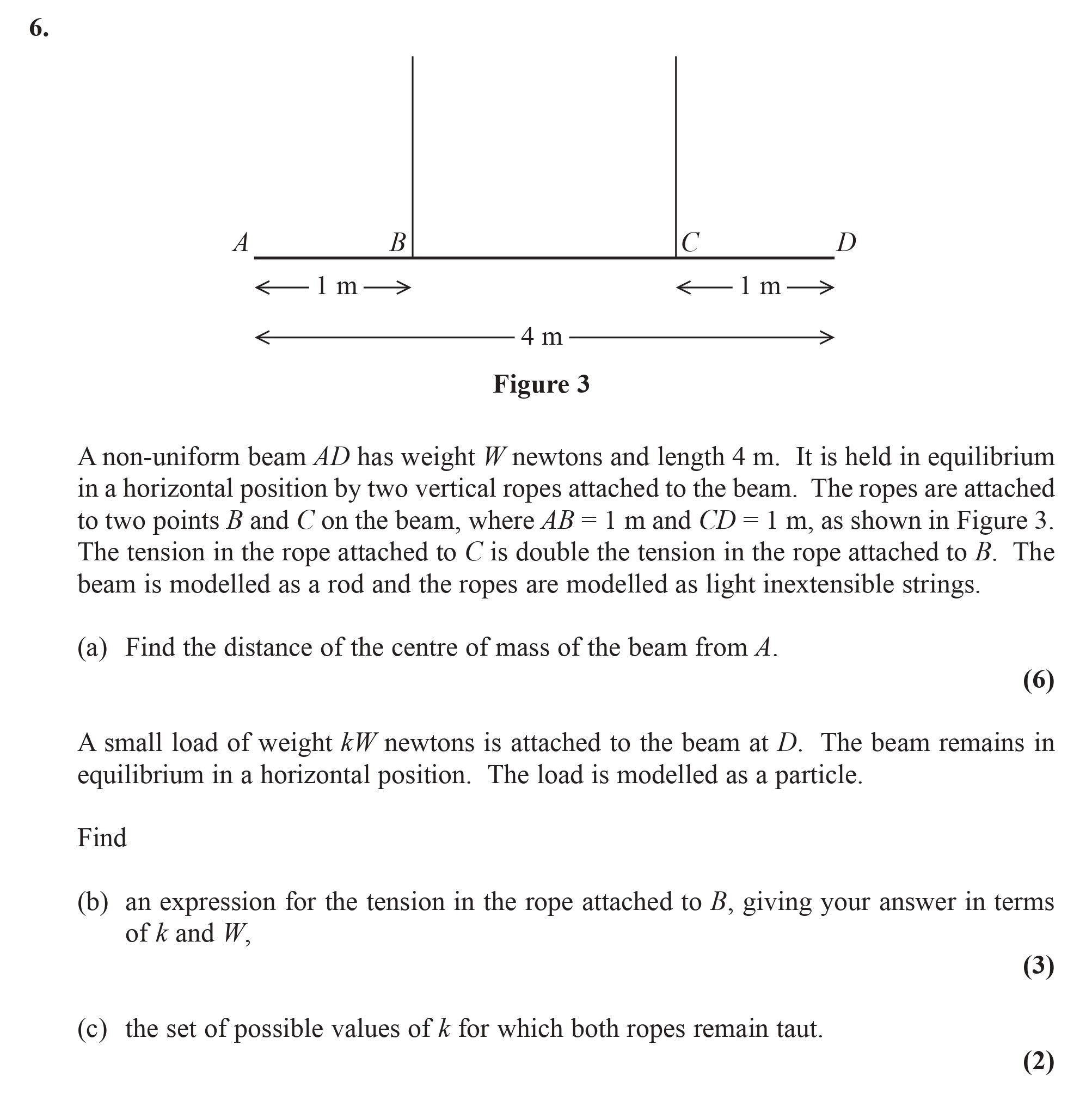
A-non-uniform-beam-AD-has-weight-W-newtons-and-length-4-m-Edexcel-A-Level Maths Mechanics-Question 6-2014-Paper 1.png

A non-uniform beam AD has weight W newtons and length 4 m. It is held in equilibrium in a horizontal position by two vertical ropes attached to the beam. The ropes a... show full transcript

Worked Solution & Example Answer:A non-uniform beam AD has weight W newtons and length 4 m - Edexcel - A-Level Maths Mechanics - Question 6 - 2014 - Paper 1

Step 1

Find the distance of the centre of mass of the beam from A.

96%

114 rated

Answer

To determine the distance of the centre of mass (d) from point A, we can use the formula for a uniform rod:

  1. The beam is 4 m long with sections of 1 m each at points A and D, leaving a segment of 2 m in the middle.

  2. Considering the weight W acting at the centre of gravity (2 m from A), the equation can be set up as:

    T+2T=WT + 2T = W

    Here, T is the tension in the rope attached to B.

  3. Rearranging gives:

    T=W3T = \frac{W}{3}

    The forces balance at the point of interest.

  4. Therefore, substituting back, the distance (d) from A can be calculated as:

    d=23⋅4=83extmd = \frac{2}{3} \cdot 4 = \frac{8}{3} ext{ m}

Step 2

an expression for the tension in the rope attached to B, giving your answer in terms of k and W.

99%

104 rated

Answer

To find the tension in the rope attached to B, we return to our earlier established relationships and consider the additional load:

  1. Sum of vertical forces gives:

    TB+2(kW)=WT_B + 2(kW) = W

    This represents tension T_B plus double the load attached.

  2. Rearranging to solve for T_B leads to:

    TB=W−2(kW)=W(1−2k)T_B = W - 2(kW) = W(1 - 2k)

    This is the expression for tension in the rope at B.

Step 3

the set of possible values of k for which both ropes remain taut.

96%

101 rated

Answer

For both ropes to remain taut, T_B must be greater than 0.

  1. Setting the inequality:

    W(1−2k)>0W(1 - 2k) > 0

    Simplifying leads to:

    1−2k>01 - 2k > 0

  2. Solving this inequality yields:

    0<k<120 < k < \frac{1}{2}

    Therefore, k must lie between 0 and \frac{1}{2} for the conditions to hold.

Join the A-Level students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;