Photo AI
A particle of mass m kg is attached at C to two light inextensible strings AC and BC - Edexcel - A-Level Maths Mechanics - Question 3 - 2010 - Paper 1
Question 3
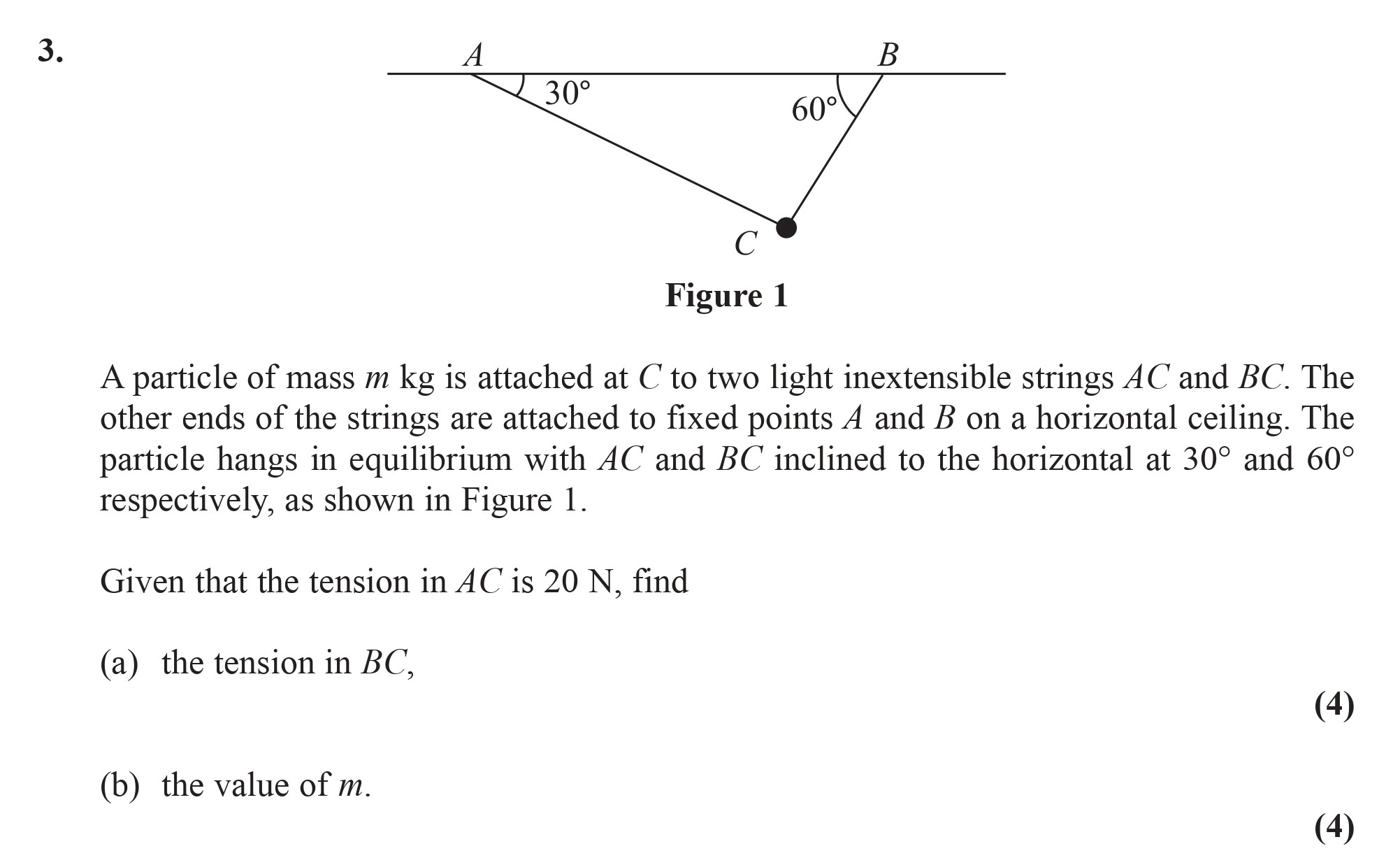
A particle of mass m kg is attached at C to two light inextensible strings AC and BC. The other ends of the strings are attached to fixed points A and B on a horizon... show full transcript
Worked Solution & Example Answer:A particle of mass m kg is attached at C to two light inextensible strings AC and BC - Edexcel - A-Level Maths Mechanics - Question 3 - 2010 - Paper 1
Step 1
(a) the tension in BC,
Answer
To find the tension in string BC (represented as T), we can analyze the horizontal components of the forces acting on the particle at point C. Since the system is in equilibrium, the horizontal forces must balance each other.
The horizontal component of the tension in AC can be calculated as:
T_{AC} imes ext{cos}(30°) = 20 imes rac{ ext{√3}}{2} = 10 ext{√3}
Now, for the tension T in BC, the horizontal component is:
T imes ext{cos}(60°) = T imes rac{1}{2}
Setting these two horizontal components equal gives:
10 ext{√3} = rac{T}{2}
Thus, to find T, we get:
Step 2
(b) the value of m.
Answer
In this part, we will consider the vertical components. The vertical components must also be in equilibrium, meaning the sum of the upward forces equals the downward force due to gravity.
The downward force acting on the mass is represented as mg, and the upward forces are due to the vertical components of the tensions in the strings:
Substituting the known values, we first calculate:
- ext{sin}(30°) = rac{1}{2}
- ext{sin}(60°) = rac{ ext{√3}}{2}
Thus, substituting T = 20 ext{√3}:
mg = 20 imes rac{1}{2} + 20 ext{√3} imes rac{ ext{√3}}{2}
This simplifies to:
Finally, solving for m, we have:
m = rac{40}{g}
Assuming g ≈ 9.8 m/s², we find:
