Photo AI
Figure 2 shows part of the curve with equation $y = (2x - 1) \tan 2x$, $0 < x < \frac{\pi}{4}$ The curve has a minimum at the point P - Edexcel - A-Level Maths Pure - Question 6 - 2006 - Paper 4
Question 6
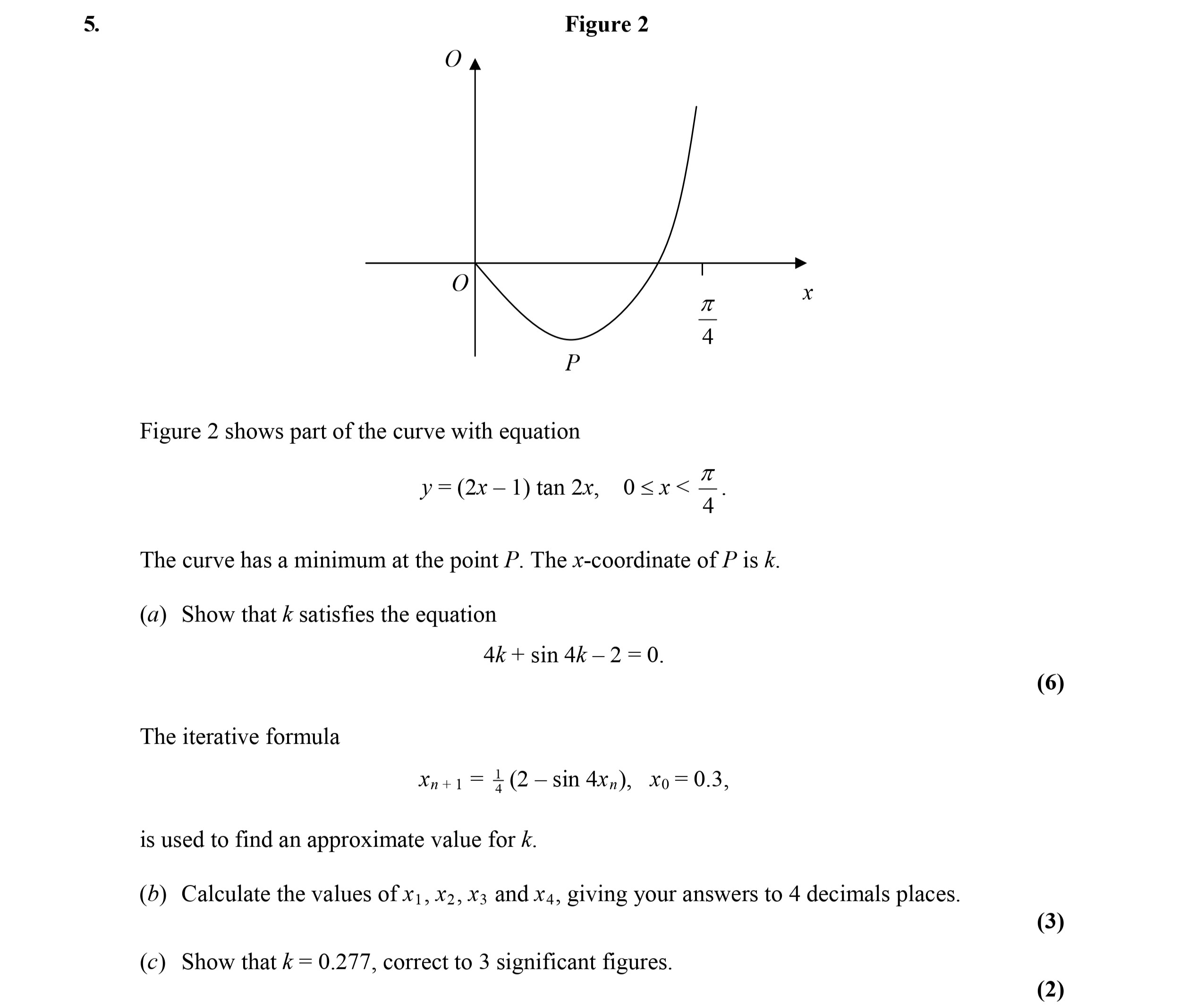
Figure 2 shows part of the curve with equation $y = (2x - 1) \tan 2x$, $0 < x < \frac{\pi}{4}$ The curve has a minimum at the point P. The x-coordinate of P i... show full transcript
Worked Solution & Example Answer:Figure 2 shows part of the curve with equation $y = (2x - 1) \tan 2x$, $0 < x < \frac{\pi}{4}$ The curve has a minimum at the point P - Edexcel - A-Level Maths Pure - Question 6 - 2006 - Paper 4
Step 1
Show that k satisfies the equation
Answer
To find the x-coordinate k of point P, we start by differentiating the given equation using the product rule:
Next, we find the critical points by setting the derivative to zero:
We also simplify using ( \tan 2x = \frac{\sin 2x}{\cos 2x} ) and ( \sec^2 2x = \frac{1}{\cos^2 2x} ).
Rearranging gives us:
From this, we find that either ( \sin 2x = 0 ) or ( 2x - 1 = 0 ). Therefore, solving for x yields:
Setting the equation ( 4k + \sin 4k - 2 = 0 ) completes our requirement.
Step 2
Step 3
Show that k = 0.277, correct to 3 significant figures
Answer
To show that ( k = 0.277 ) to 3 significant figures, we can analyze the calculated values from the iterative method:
- The values converge between ( 0.2768 ) and ( 0.2790 ).
- When rounding ( 0.2774 ) to three significant figures, we see it maintains a value of 0.277. Hence, this confirms our value of k as required.
