Photo AI
Figure 1 shows a sketch of part of the curve with equation $y = \frac{10}{2x + 5\sqrt{x}}$, where $x > 0$ - Edexcel - A-Level Maths Pure - Question 4 - 2014 - Paper 7
Question 4
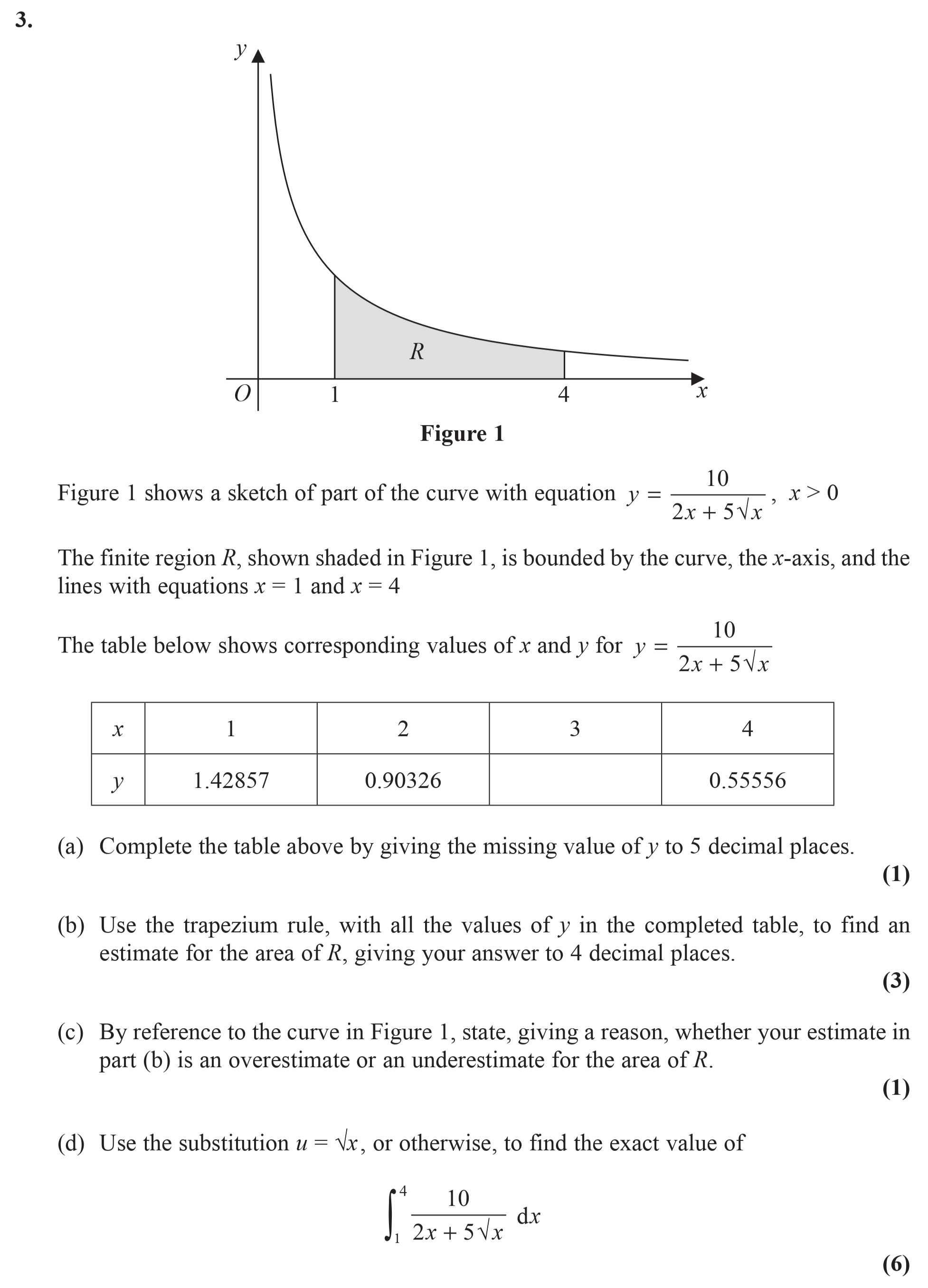
Figure 1 shows a sketch of part of the curve with equation $y = \frac{10}{2x + 5\sqrt{x}}$, where $x > 0$. The finite region $R$, shown shaded in Figure 1, is b... show full transcript
Worked Solution & Example Answer:Figure 1 shows a sketch of part of the curve with equation $y = \frac{10}{2x + 5\sqrt{x}}$, where $x > 0$ - Edexcel - A-Level Maths Pure - Question 4 - 2014 - Paper 7
Step 1
Step 2
Use the trapezium rule, with all the values of y in the completed table, to find an estimate for the area of R, giving your answer to 4 decimal places.
Answer
The trapezium rule states:
For our table, we have:
h = 1 (the width between each value),
Calculating gives:
\approx \frac{1}{2} \times 5.03639 = 2.518195 \approx 2.5182$$Step 3
By reference to the curve in Figure 1, state, giving a reason, whether your estimate in part (b) is an overestimate or an underestimate for the area of R.
Answer
Since the trapezium rule approximates the area under the curve by using straight lines to connect the values of , if the actual curve is concave (bending downwards) like in Figure 1, then our estimation will be an overestimate. This is because the trapezoids will extend above the curve in the regions .
Step 4
Use the substitution u = √x, or otherwise, to find the exact value of ∫_1^4 10/(2x + 5√x) dx
Answer
Using the substitution , hence and . The limits of integration change from (where ) to (where ).
The integral becomes:
This simplifies to:
Now integrating:
Calculating from to :
Thus, the exact value is:
