Photo AI
Figure 3 shows a sketch of the curve with equation $y = (x - 1) ext{ln} x$, $x > 0$ - Edexcel - A-Level Maths Pure - Question 7 - 2006 - Paper 6
Question 7
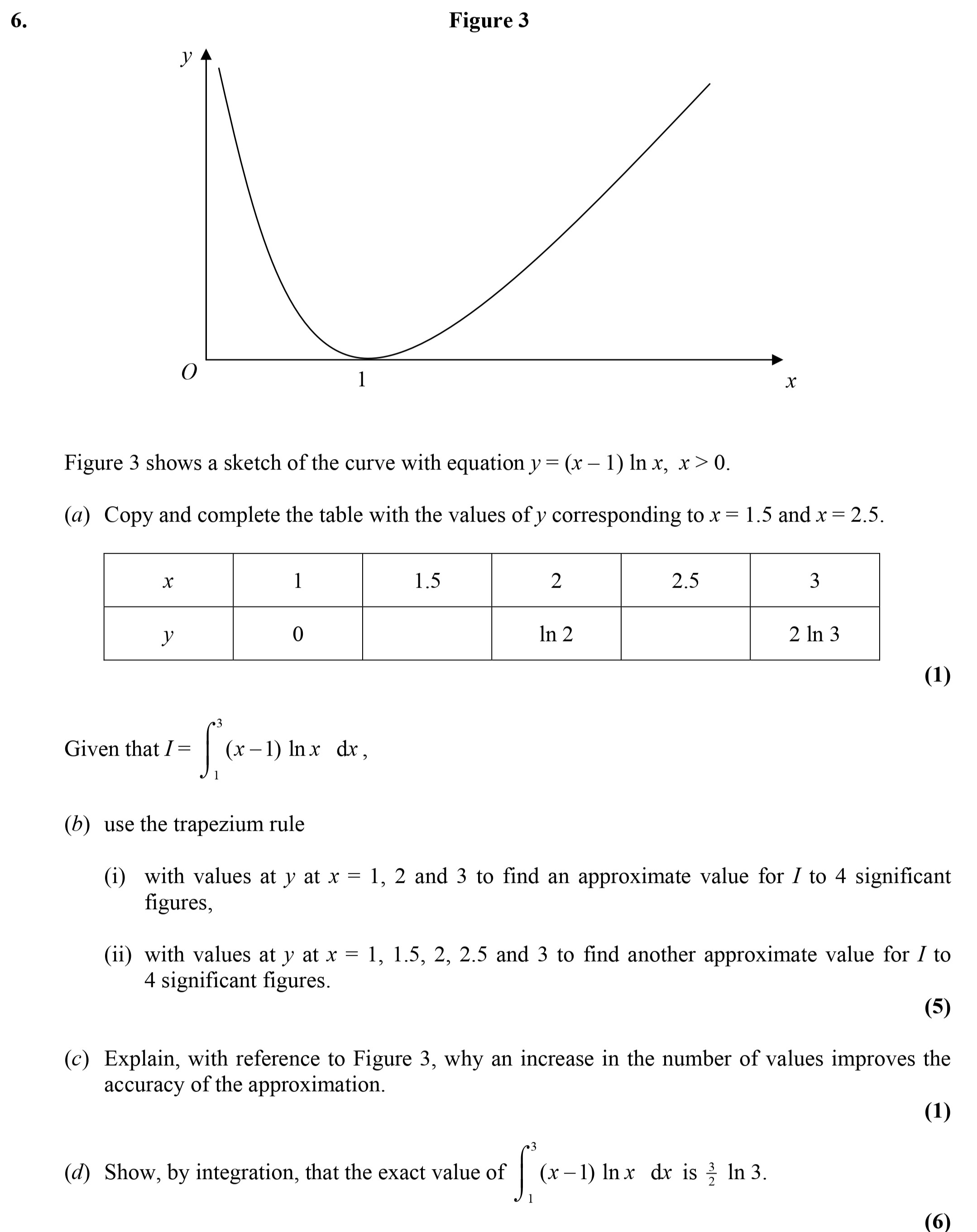
Figure 3 shows a sketch of the curve with equation $y = (x - 1) ext{ln} x$, $x > 0$. (a) Copy and complete the table with the values of $y$ corresponding to $x = 1... show full transcript
Worked Solution & Example Answer:Figure 3 shows a sketch of the curve with equation $y = (x - 1) ext{ln} x$, $x > 0$ - Edexcel - A-Level Maths Pure - Question 7 - 2006 - Paper 6
Step 1
Step 2
use the trapezium rule (i) with values at $y$ at $x = 1, 2$ and $3$ to find an approximate value for $I$ to 4 significant figures
Answer
Using the trapezium rule formula:
where is the width between x values (which is 1 in this case), (for ), , and .
Calculating:
Thus, approximating gives .
Step 3
Step 4
Explain, with reference to Figure 3, why an increase in the number of values improves the accuracy of the approximation
Answer
Increasing the number of points used in the trapezium rule allows for a better approximation of the area under the curve, leading to reduced errors in estimation. In Figure 3, as the number of segments increases, the trapezoids used to approximate the area align more closely with the curve. This behavior reduces the overestimation and underestimation effects typical of using fewer segments, resulting in a more accurate overall estimation of the integral.
Step 5
Show, by integration, that the exact value of $\int (x - 1) \text{ln} x \, dx$ is $\frac{1}{2} \text{ln} 3$
Answer
To solve the integral:
Using integration by parts where we let:
Then we find:
Now substituting these into the integration by parts formula:
Therefore:
Continuing with the integrals and evaluating at limits from 1 to 3, we arrive at the exact value of .
