Figure 1 shows a sketch of the graph of $y = f(x)$. The graph intersects the y-axis at the point $(0, 1)$ and the point $A(2, 3)$ is the maximum turning point. Sketch, on separate axes, the graphs of (i) $y = f(-x) + 1$, (ii) $y = f(x + 2) + 3$, (iii) $y = 2f(2x)$. On each sketch, show the coordinates of the point at which your graph intersects the y-axis and the coordinates to which $A$ is transformed.

Photo AI

Figure 1 shows a sketch of the graph of $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 7 - 2010 - Paper 2

Question 7

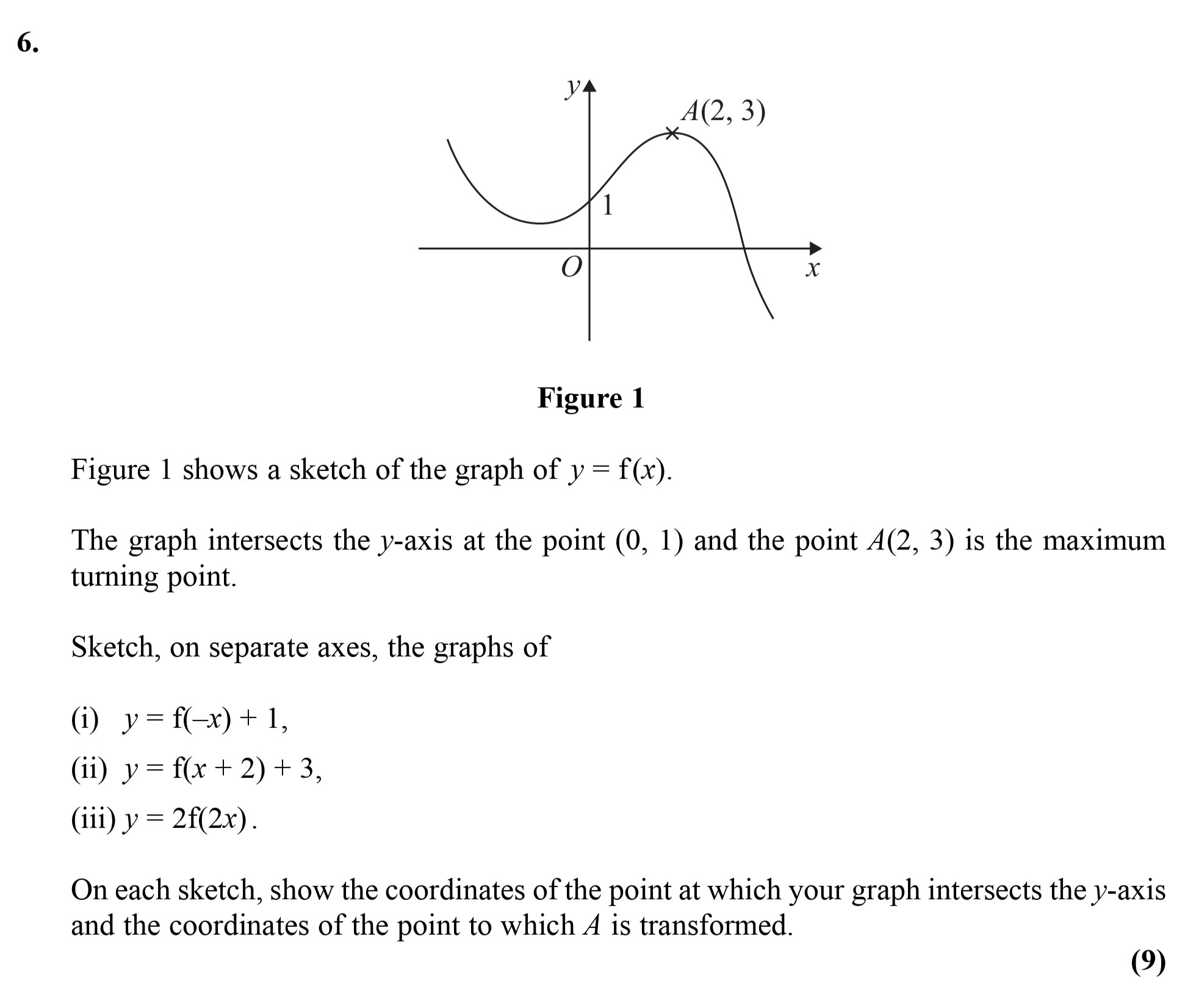
Figure 1 shows a sketch of the graph of $y = f(x)$. The graph intersects the y-axis at the point $(0, 1)$ and the point $A(2, 3)$ is the maximum turning point. S... show full transcript

Worked Solution & Example Answer:Figure 1 shows a sketch of the graph of $y = f(x)$ - Edexcel - A-Level Maths Pure - Question 7 - 2010 - Paper 2

Step 1

y = f(-x) + 1

96%

114 rated

Answer

The graph of $y = f(-x) + 1$ reflects $f(x)$ across the y-axis and shifts it up by 1 unit.

The y-intercept becomes $(0, 2)$ , as the original graph meets the y-axis at $(0, 1)$ and is shifted up.
The maximum point A ( $A(2, 3)$ ) transforms to $A'(-2, 4)$ due to the reflection and translation.

Thus, the coordinates of the transformed point are $A'(-2, 4)$ .

Step 2

y = f(x + 2) + 3

99%

104 rated

Answer

For the equation $y = f(x + 2) + 3$ , the graph shifts left by 2 units and up by 3 units.

The y-intercept, originally at $(0, 1)$ , will now be at $(-2, 4)$ before the upward translation.
The maximum point A transforms to $A'(0, 6)$ , following the same left-shift and upward shift.

Hence, the transformed point A' is $(0, 6)$ .

Step 3

y = 2f(2x)

96%

101 rated

Answer

In the equation $y = 2f(2x)$ , we have a horizontal compression by a factor of 2 and a vertical stretch by a factor of 2.

The y-intercept alters, with the original at $(0, 1)$ becoming $(0, 2)$ , since it is multiplied by 2.
The point A transforms to $A'(1, 6)$ based on the transformation rules.

So, the final coordinates of the transformed point A' are $(1, 6)$ .

Join the A-Level students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;