Photo AI
Figure 2 shows a sketch of part of the graph $y = f(x)$, where $f(x) = 2/3 - |x| + 5, \, x > 0$ - Edexcel - A-Level Maths Pure - Question 12 - 2017 - Paper 2
Question 12
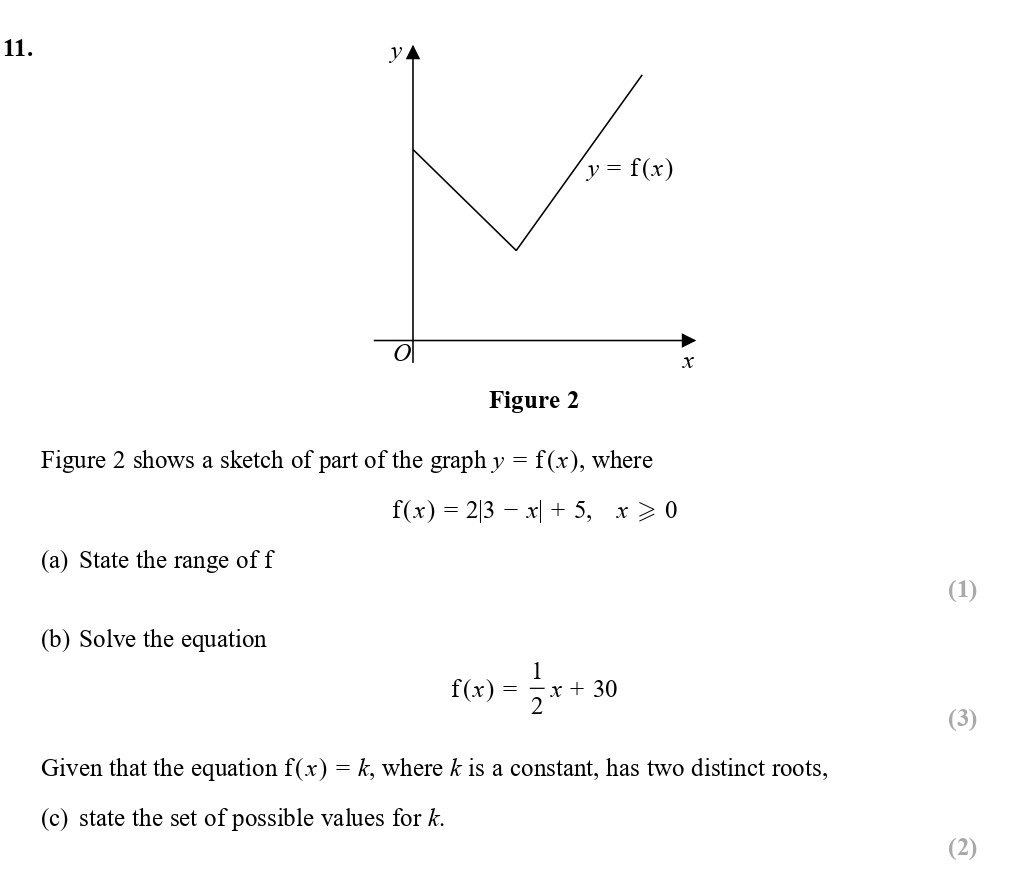
Figure 2 shows a sketch of part of the graph $y = f(x)$, where $f(x) = 2/3 - |x| + 5, \, x > 0$. (a) State the range of $f$. (b) Solve the equation $f(x) = \frac{1... show full transcript
Worked Solution & Example Answer:Figure 2 shows a sketch of part of the graph $y = f(x)$, where $f(x) = 2/3 - |x| + 5, \, x > 0$ - Edexcel - A-Level Maths Pure - Question 12 - 2017 - Paper 2
Step 1
Step 2
Solve the equation
Answer
To solve the equation , we first substitute the function:
This simplifies to:
Next, we isolate the absolute value term:
Perform the calculations for the right side:
Multiply through by 3 to eliminate fractions:
This leads to working through both cases of the absolute value and solving for x, concluding with:
Step 3
state the set of possible values for k
Answer
For the equation to have two distinct roots, the line must intersect the graph of in two distinct places. From our earlier analysis: Since achieves a maximum of (which is approximately 5.67) when and extends to as increases, the range of must satisfy:
Thus, the set of possible values for is:
