Photo AI
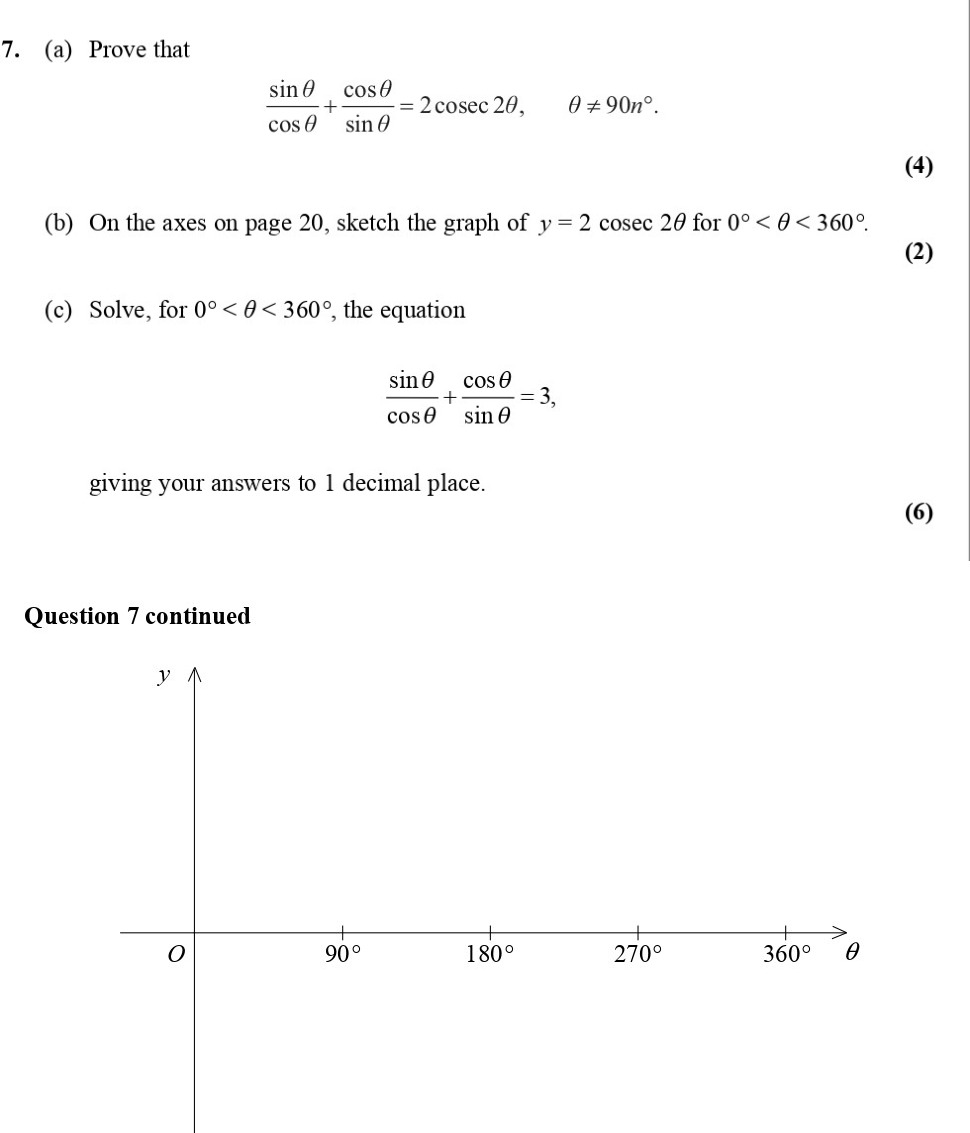
7. (a) Prove that $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} + \frac{\sin^2 \theta}{\sin \theta} = 2 \csc 2\theta, \quad \theta \neq 90^\circ.$$ (b) On the axes on page 20, sketch the graph of $$y = 2 \csc 2\theta$$ for $$0^\circ < \theta < 360^\circ.$$ (c) Solve, for $$0^\circ < \theta < 360^\circ$$, the equation $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} \cdot \frac{\cos \theta}{\sin \theta} = 3,$$ giving your answers to 1 decimal place. - Edexcel - A-Level Maths Pure - Question 1 - 2007 - Paper 5
Question 1
7. (a) Prove that $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} + \frac{\sin^2 \theta}{\sin \theta} = 2 \csc 2\theta, \quad \theta \neq 90^\circ.$$ (b) ... show full transcript
Worked Solution & Example Answer:7. (a) Prove that $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} + \frac{\sin^2 \theta}{\sin \theta} = 2 \csc 2\theta, \quad \theta \neq 90^\circ.$$ (b) On the axes on page 20, sketch the graph of $$y = 2 \csc 2\theta$$ for $$0^\circ < \theta < 360^\circ.$$ (c) Solve, for $$0^\circ < \theta < 360^\circ$$, the equation $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} \cdot \frac{\cos \theta}{\sin \theta} = 3,$$ giving your answers to 1 decimal place. - Edexcel - A-Level Maths Pure - Question 1 - 2007 - Paper 5
Step 1
Prove that $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} + \frac{\sin^2 \theta}{\sin \theta} = 2 \csc 2\theta$$
Answer
To prove the equation, start by rewriting the left-hand side:
-
Combine terms by finding a common denominator:
-
Factor out from the numerator:
-
Using the double angle identity, recall that . Thus, we can express this as:
-
Conclude that this equals the right-hand side: , thereby proving the equation.
Step 2
On the axes on page 20, sketch the graph of $$y = 2 \csc 2\theta$$ for $$0^\circ < \theta < 360^\circ$$
Answer
To sketch the graph:
-
Identify the asymptotes where for , which gives asymptotes at: .
-
Mark the points where the function attains its maximum and minimum, which occur at resulting in values of 2 and -2.
-
Plot the curve, noting the general shape of the cosecant function - it will have branches extending infinitely in both positive and negative directions.
Step 3
Solve, for $$0^\circ < \theta < 360^\circ$$, the equation $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} \cdot \frac{\cos \theta}{\sin \theta} = 3$$
Answer
To solve the equation:
-
Rearrange and simplify the equation: .
-
Therefore, implies: .
-
Find the general solution for : which gives: .
-
Hence, for , divide each result by 2:
Format the answers to 1 decimal place as:- , , , .
