Photo AI
Figure 4 shows a solid brick in the shape of a cuboid measuring $2x$ cm by $x$ cm by $y$ cm - Edexcel - A-Level Maths Pure - Question 2 - 2007 - Paper 2
Question 2
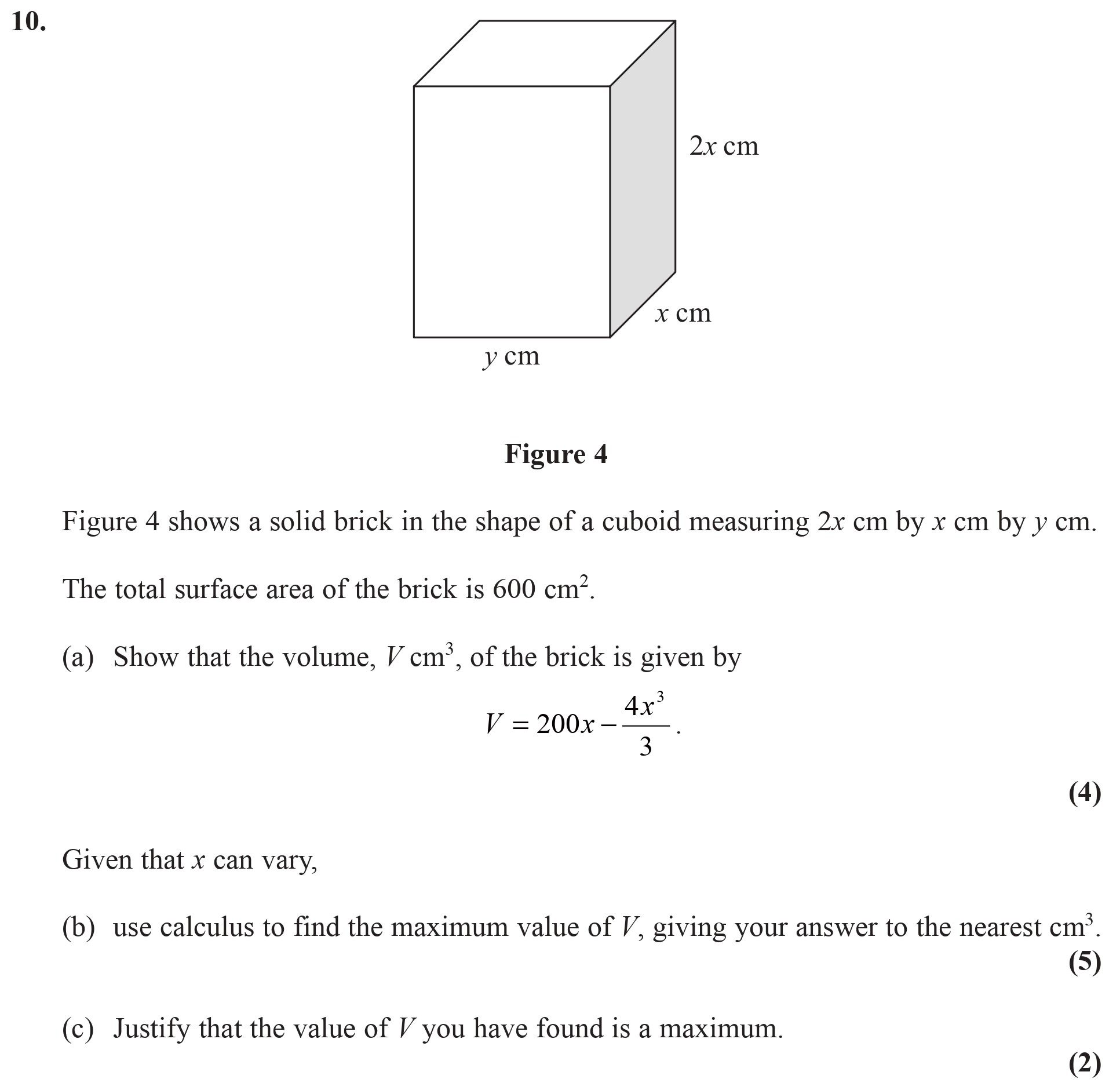
Figure 4 shows a solid brick in the shape of a cuboid measuring $2x$ cm by $x$ cm by $y$ cm. The total surface area of the brick is 600 cm$^2$. (a) Show that the v... show full transcript
Worked Solution & Example Answer:Figure 4 shows a solid brick in the shape of a cuboid measuring $2x$ cm by $x$ cm by $y$ cm - Edexcel - A-Level Maths Pure - Question 2 - 2007 - Paper 2
Step 1
Show that the volume, $V$ cm$^3$, of the brick is given by
Answer
To find the volume of the brick, we start by expressing the total surface area in terms of and . The total surface area for the cuboid is given by:
Setting this equal to 600 cm gives us:
From this equation, we can solve for :
\ \ y = \frac{600 - 4x^2}{6x} = \frac{100 - \frac{2}{3}x^2}{x} = \frac{200 - \frac{4}{3}x^2}{3}.$$ Substituting $y$ into the volume formula: $$V = 2xy^2 = 2x \left(\frac{600 - 4x^2}{6x}\right)^2 = 2x \cdot \frac{(600 - 4x^2)^2}{36x^2} = \frac{200(600 - 4x^2)}{6} = \frac{200xy - 4x^3}{3}.$$Step 2
use calculus to find the maximum value of $V$, giving your answer to the nearest cm$^3$
Answer
To find the maximum volume, we will first differentiate with respect to :
Set the derivative equal to zero to find the critical points:
Substituting back into the equation for gives:
Now substituting these values into the volume:
Step 3
Justify that the value of $V$ you have found is a maximum
Answer
To confirm that we've found a maximum, we calculate the second derivative:
Substituting our critical point :
Since this value is negative, it indicates that the function is concave down, confirming that we have a local maximum at this point.
