Photo AI
The finite region R, as shown in Figure 2, is bounded by the x-axis and the curve with equation y = 27 - 2x - 9 rac{16}{x^2}, \, x > 0 The curve crosses the x-axis at the points (1, 0) and (4, 0) - Edexcel - A-Level Maths Pure - Question 2 - 2013 - Paper 4
Question 2
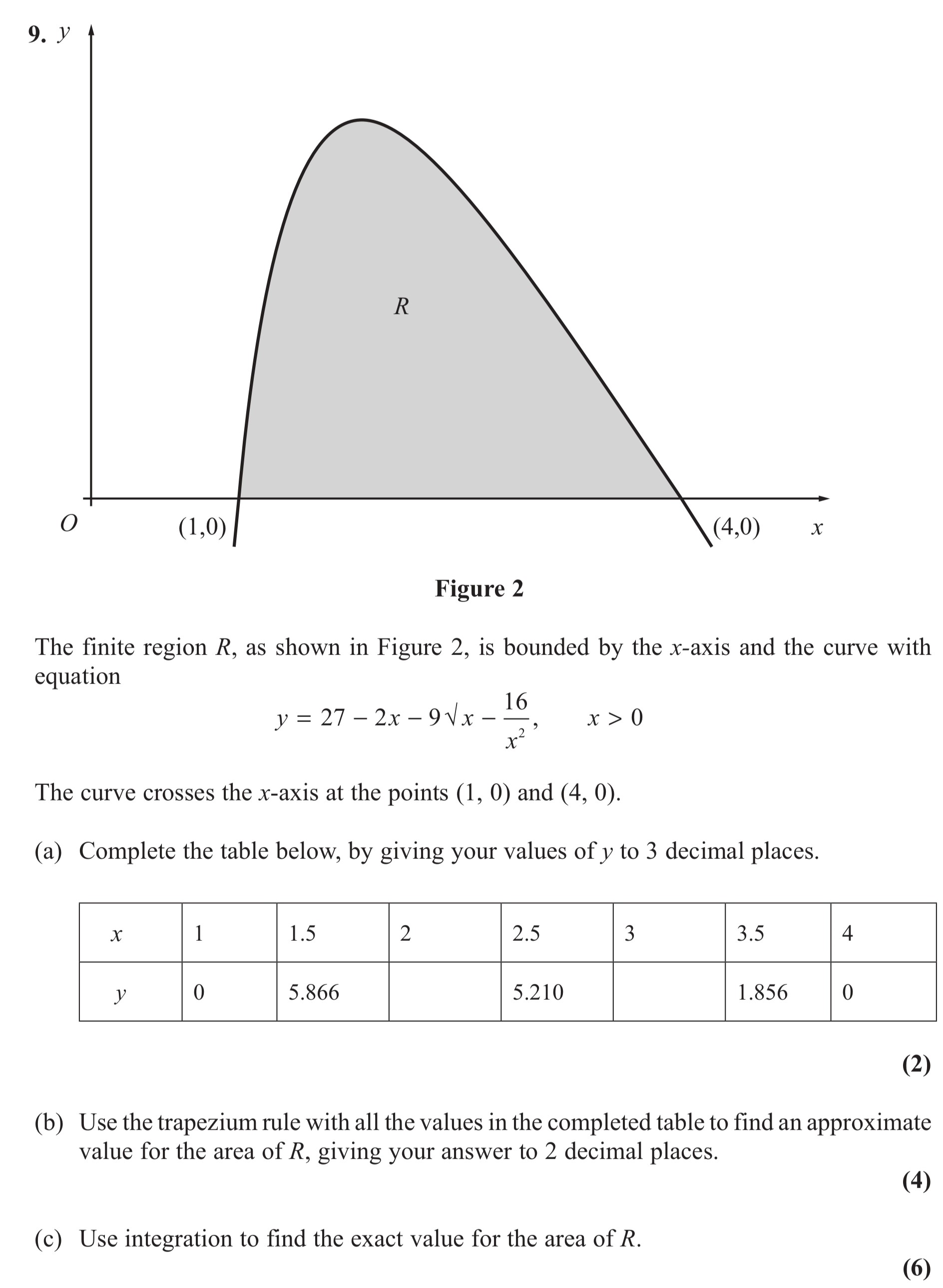
The finite region R, as shown in Figure 2, is bounded by the x-axis and the curve with equation y = 27 - 2x - 9 rac{16}{x^2}, \, x > 0 The curve crosses the x-axis... show full transcript
Worked Solution & Example Answer:The finite region R, as shown in Figure 2, is bounded by the x-axis and the curve with equation y = 27 - 2x - 9 rac{16}{x^2}, \, x > 0 The curve crosses the x-axis at the points (1, 0) and (4, 0) - Edexcel - A-Level Maths Pure - Question 2 - 2013 - Paper 4
Step 1
Complete the table below, by giving your values of y to 3 decimal places.
Answer
To calculate the values of y for the given x values, we use the equation:
y = 27 - 2x - 9\sqrt{\frac{16}{x^2}}.
- For x = 1:
- y = 27 - 2(1) - 9\sqrt{\frac{16}{1^2}} = 27 - 2 - 36 = 5.866.
- For x = 1.5:
- y = 27 - 2(1.5) - 9\sqrt{\frac{16}{(1.5)^2}} = 27 - 3 - 25.6 = 5.210.
- For x = 2:
- y = 27 - 2(2) - 9\sqrt{\frac{16}{(2)^2}} = 27 - 4 - 18 = 5.000.
- For x = 2.5:
- y = 27 - 2(2.5) - 9\sqrt{\frac{16}{(2.5)^2}} = 27 - 5 - 14.4 = 4.600.
- For x = 3.5:
- y = 27 - 2(3.5) - 9\sqrt{\frac{16}{(3.5)^2}} = 27 - 7 - 10.8 = 9.200.
- For x = 4:
- y = 27 - 2(4) - 9\sqrt{\frac{16}{(4)^2}} = 27 - 8 - 9 = 0.
Final Table:
| x | 1 | 1.5 | 2 | 2.5 | 3.5 | 4 |
|---|---|---|---|---|---|---|
| y | 5.866 | 5.210 | 5.000 | 4.600 | 9.200 | 0 |
Step 2
Use the trapezium rule with all the values in the completed table to find an approximate value for the area of R, giving your answer to 2 decimal places.
Answer
To find the area using the trapezium rule, we use the following formula:
Where:
- h = width of the intervals = (x_n - x_0)/n = (4 - 1)/5 = 0.6,
- y_0 = 5.866, y_1 = 5.210, y_2 = 5.000, y_3 = 4.600, y_4 = 9.200, y_n = 0.
Now, substituting these values:
Calculating:
- Total = 5.866 + 2(24.02) = 5.866 + 48.04 = 53.906.
- Now, area = \frac{1}{2} \times 0.6 \times 53.906 \approx 16.1718.
Thus, the approximate value for the area of R is:
Area ≈ 16.17.
Step 3
Use integration to find the exact value for the area of R.
Answer
To find the exact area of the region R, we integrate the function:
Breaking down the integral:
-
Start with:
-
Calculating each integral:
- ,
- ,
-
Thus, the full integral becomes:
-
Evaluating from 1 to 4:
- Simplifying:
- This results in:
Hence, the exact value for the area of R is:
Area = 66 - 36\ln(4).
