Photo AI
Figure 4 shows a closed letter box ABFEHGCD, which is made to be attached to a wall of a house - Edexcel - A-Level Maths Pure - Question 1 - 2014 - Paper 1
Question 1
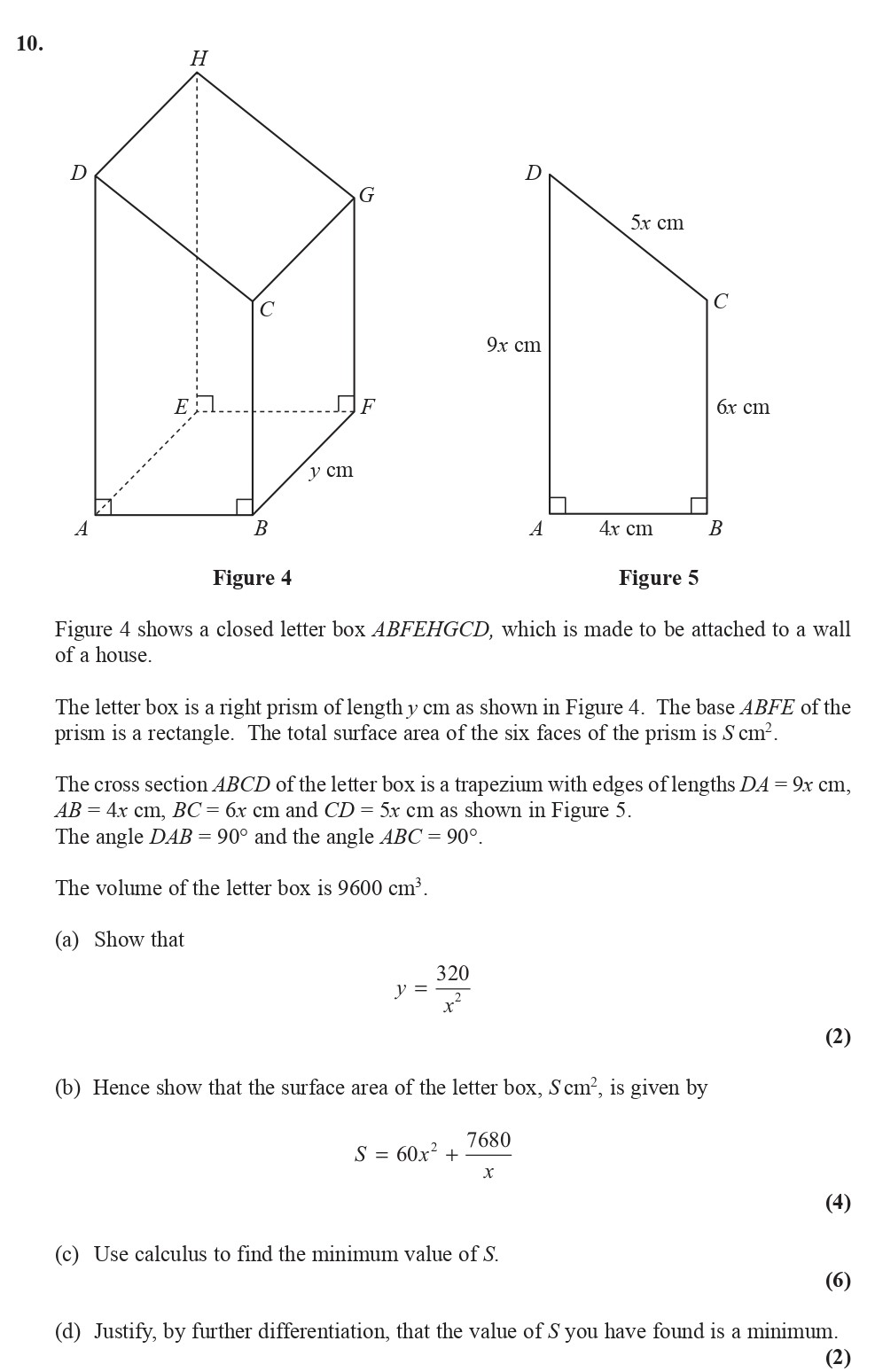
Figure 4 shows a closed letter box ABFEHGCD, which is made to be attached to a wall of a house. The letter box is a right prism of length y cm as shown in Figure 4.... show full transcript
Worked Solution & Example Answer:Figure 4 shows a closed letter box ABFEHGCD, which is made to be attached to a wall of a house - Edexcel - A-Level Maths Pure - Question 1 - 2014 - Paper 1
Step 1
Show that \( y = \frac{320}{x^2} \)
Answer
To find ( y ) in terms of ( x ), we start from the volume formula for the letter box, which is:
Substituting in values, we have:
( V = (4 + 5) \cdot \frac{1}{2} (9 + 6) \cdot y = 9 \cdot 7.5 \cdot y = 67.5y ) cm³.
Setting ( V = 9600 ) cm³ gives us:
From which we can solve for ( y ):
. This confirms the required relation.
Step 2
Hence show that the surface area of the letter box, S cm², is given by \( S = 60x + 7680 \)
Answer
The total surface area ( S ) of the letter box includes the areas of the top, bottom, and sides:
-
Area of the sides: There are 2 rectangles along the length:
- Area = ( 9y + 4y + 6y + 5y = 24y )
- Therefore, Area = ( 24 \frac{320}{x^2} )
-
Area of the top and bottom: Each is a rectangle:
- Each has an area of ( 4x )
- Total = ( 2 * 4x = 8x )
Adding these, we have:
Step 3
Use calculus to find the minimum value of S.
Answer
To minimize ( S = 60x + 7680 ), we can take the derivative and set it to zero:
-
Calculate the derivative:
- ( S' = 60 + 0 = 60 ), where the derivative is equal to zero at critical points. Since there are no critical points, we check the second derivative:
-
Take the second derivative:
- ( S'' = 0 ), indicating a linear function. It does not have a minimum this way, so we also need to analyze its behavior.
Since the linear function is increasing, we evaluate at the endpoints to find the minimum.
Step 4
Justify, by further differentiation, that the value of S you have found is a minimum.
Answer
Given that ( S = 60x + 7680 ) is a linear function where the slope (60) is positive, there is no turning point present. Therefore, there is no minimum value from calculus. Since all values of ( S ) increase as x increases, the minimum occurs at the boundary when x is smallest. Further differentiation confirms that no critical points which yield a minimum exist.
