Figure 2 shows a sketch of part of the curve with equation y = 4x³ + 9x² - 30x - 8, −0.5 ≤ x ≤ 2.2 The curve has a turning point at the point A. (a) Using calculus, show that the x coordinate of A is 1. The curve crosses the x-axis at the points B(2, 0) and C(−rac{1}{4}, 0). The finite region R, shown shaded in Figure 2, is bounded by the curve, the line AB, and the x-axis. (b) Use integration to find the area of the finite region R, giving your answer to 2 decimal places.

A-Level Edexcel Maths Pure Circles: Figure 2 shows a sketch of part

Figure 2 shows a sketch of part of the curve with equation y = 4x³ + 9x² - 30x - 8, −0.5 ≤ x ≤ 2.2 The curve has a turning point at the point A - Edexcel - A-Level Maths Pure - Question 2 - 2015 - Paper 2

Question 2

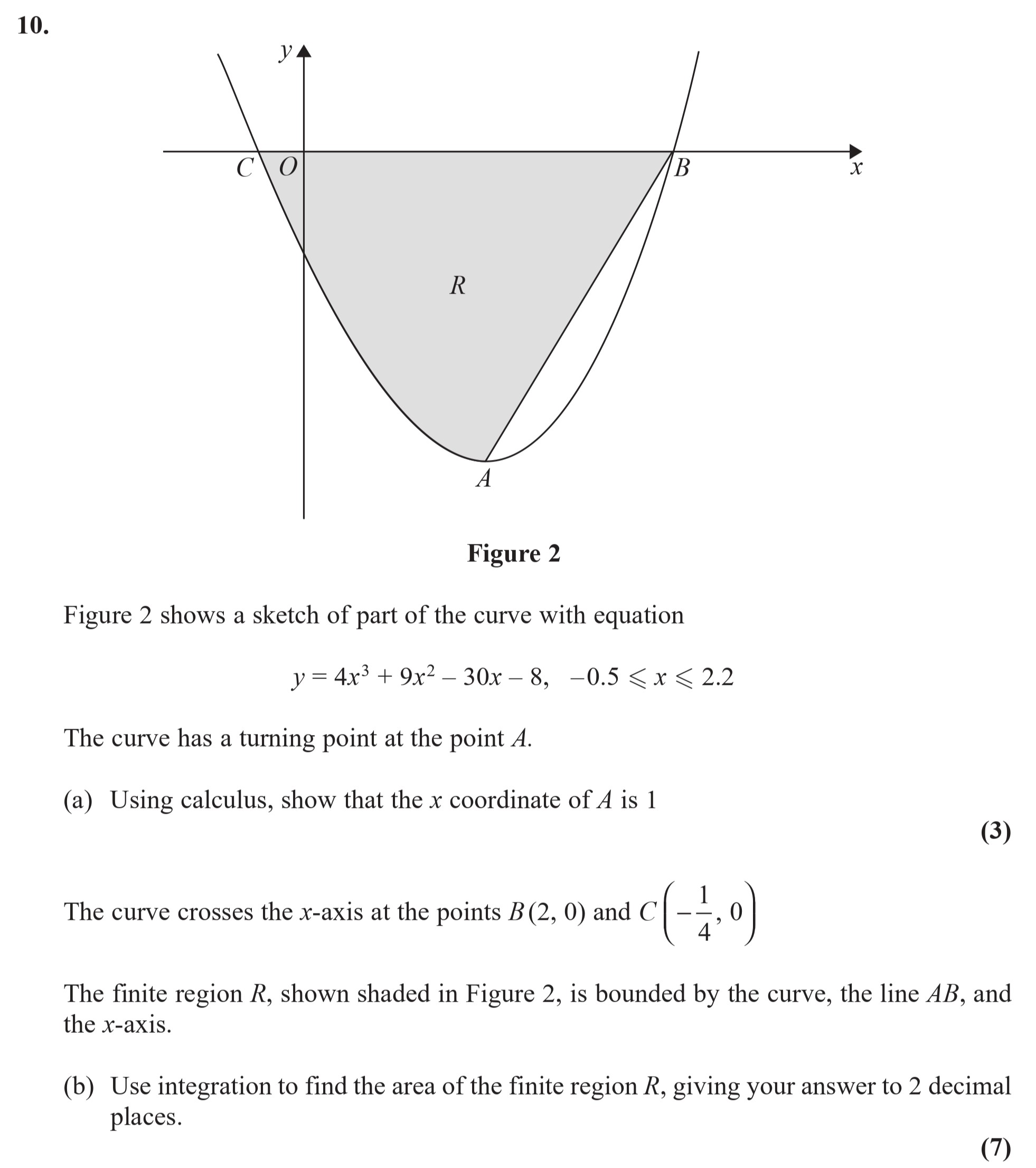
Figure-2-shows-a-sketch-of-part-of-the-curve-with-equation--y-=-4x³-+-9x²---30x---8,--−0.5-≤-x-≤-2.2--The-curve-has-a-turning-point-at-the-point-A-Edexcel-A-Level Maths Pure-Question 2-2015-Paper 2.png

Figure 2 shows a sketch of part of the curve with equation y = 4x³ + 9x² - 30x - 8, −0.5 ≤ x ≤ 2.2 The curve has a turning point at the point A. (a) Using calcul... show full transcript

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation y = 4x³ + 9x² - 30x - 8, −0.5 ≤ x ≤ 2.2 The curve has a turning point at the point A - Edexcel - A-Level Maths Pure - Question 2 - 2015 - Paper 2

Step 1

Using calculus, show that the x coordinate of A is 1.

96%

114 rated

Answer

To find the turning point A, we first differentiate the curve's equation:

$y' = 12x^2 + 18x - 30$

Setting the derivative to zero:

$12x^2 + 18x - 30 = 0$

Dividing through by 6 simplifies this to:

$2x^2 + 3x - 5 = 0$

Applying the quadratic formula:

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Substituting a = 2, b = 3, and c = -5:

$x = \frac{-3 \pm \sqrt{3^2 - 4 imes 2 \times (-5)}}{2 imes 2}$

Calculating the discriminant:

$3^2 + 40 = 49$

Thus, we have:

$x = \frac{-3 \pm 7}{4}$

Calculating possible x values:

$x = \frac{4}{4} = 1$
$x = \frac{-10}{4} = -2.5$ (not in range)

Therefore, the only feasible x coordinate for point A is:

x = 1.

Step 2

Use integration to find the area of the finite region R, giving your answer to 2 decimal places.

99%

104 rated

Answer

To find the area of the finite region R, we first calculate the definite integral of the curve from x = -rac{1}{4} to x = 2:

$ext{Area} = \int_{- rac{1}{4}}^{2} (4x^3 + 9x^2 - 30x - 8) \, dx$

Calculating the antiderivative:

$= \left( x^4 + 3x^3 - 15x^2 - 8x \right) \Bigg|_{- rac{1}{4}}^{2}$

Evaluating this at the limits:

At x = 2: $= 2^4 + 3(2^3) - 15(2^2) - 8(2)$
$= 16 + 24 - 60 - 16 = -36$
At x = -rac{1}{4}: $= \left(-\frac{1}{4}\right)^4 + 3\left(-\frac{1}{4}\right)^3 - 15\left(-\frac{1}{4}\right)^2 - 8\left(-\frac{1}{4}\right)$
$= \frac{1}{256} - \frac{3}{64} - \frac{15}{16} + 2$
After evaluating, simplify to get a numerical value.

Subtract the two results to find the area: $ext{Area} = Area(2) - Area(-\frac{1}{4})$

Final calculation gives:

$32.52$ (to 2 decimal places).

Figure 2 shows a sketch of part of the curve with equation y = 4x³ + 9x² - 30x - 8, −0.5 ≤ x ≤ 2.2 The curve has a turning point at the point A - Edexcel - A-Level Maths Pure - Question 2 - 2015 - Paper 2

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation y = 4x³ + 9x² - 30x - 8, −0.5 ≤ x ≤ 2.2 The curve has a turning point at the point A - Edexcel - A-Level Maths Pure - Question 2 - 2015 - Paper 2

Using calculus, show that the x coordinate of A is 1.

Use integration to find the area of the finite region R, giving your answer to 2 decimal places.

Join the A-Level students using SimpleStudy...