Photo AI
Given that A is constant and $$\int^1_0 (3\sqrt{x} + A) \, dx = 2A^2$$ show that there are exactly two possible values for A. - Edexcel - A-Level Maths Pure - Question 12 - 2017 - Paper 2
Question 12
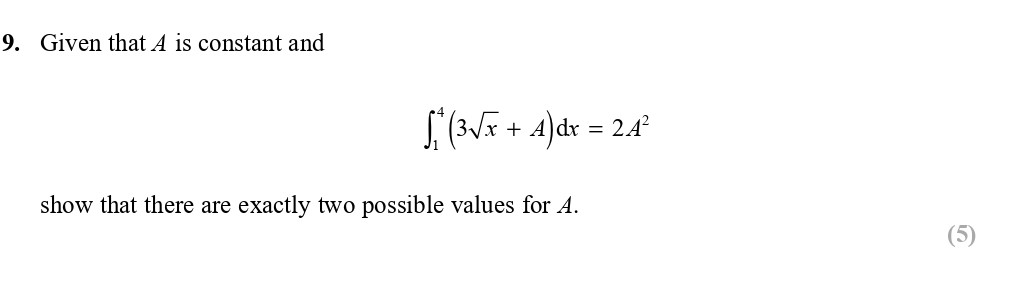
Given that A is constant and $$\int^1_0 (3\sqrt{x} + A) \, dx = 2A^2$$ show that there are exactly two possible values for A.
Worked Solution & Example Answer:Given that A is constant and $$\int^1_0 (3\sqrt{x} + A) \, dx = 2A^2$$ show that there are exactly two possible values for A. - Edexcel - A-Level Maths Pure - Question 12 - 2017 - Paper 2
Step 1
Step 2
Step 3
Step 4
