A-Level Edexcel Maths Pure Compound & Double Angle Formulae: 1. (a) By writing sin 30° as sin

1. (a) By writing sin 30° as sin(2θ + θ), show that sin 30° = 3sin θ − 4sin³ θ - Edexcel - A-Level Maths Pure - Question 1 - 2007 - Paper 6

Question 1

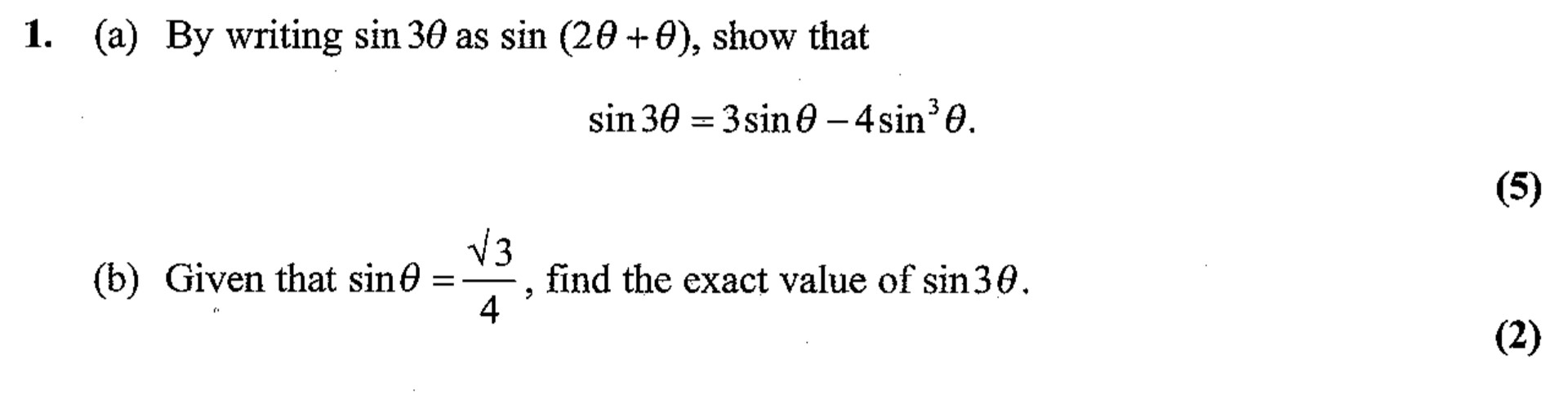
1. (a) By writing sin 30° as sin(2θ + θ), show that sin 30° = 3sin θ − 4sin³ θ. (b) Given that sin θ = \frac{\sqrt{3}}{4}, find the exact value of sin 30°.

Worked Solution & Example Answer:1. (a) By writing sin 30° as sin(2θ + θ), show that sin 30° = 3sin θ − 4sin³ θ - Edexcel - A-Level Maths Pure - Question 1 - 2007 - Paper 6

Step 1

By writing sin 30° as sin(2θ + θ), show that sin 30° = 3sin θ − 4sin³ θ.

96%

114 rated

Answer

To prove this identity, we start by applying the sine addition formula:

sin(2θ + θ) = sin(2θ)cos(θ) + cos(2θ)sin(θ).

Next, we know that:

sin(2θ) = 2sin(θ)cos(θ)

and

cos(2θ) = 1 - 2sin^2(θ).

Substituting these values into the sine addition formula, we get:

sin(2θ + θ) = (2sin(θ)cos(θ))cos(θ) + (1 - 2sin^2(θ))sin(θ).

After simplifying, we find:

sin(2θ + θ) = 2sin(θ)cos^2(θ) + sin(θ) - 2sin^3(θ).

Since $cos^2(θ) = 1 - sin^2(θ)$ , we can substitute:

sin(2θ + θ) = 2sin(θ)(1 - sin^2(θ)) + sin(θ) - 2sin^3(θ).

This simplifies to:

sin(2θ + θ) = 2sin(θ) - 2sin^3(θ) + sin(θ) - 2sin^3(θ) = 3sin(θ) - 4sin^3(θ).

Thus, we have shown that:

sin 30° = 3sin θ - 4sin³ θ.

Step 2

Given that sin θ = \frac{\sqrt{3}}{4}, find the exact value of sin 30°.

99%

104 rated

Answer

We use the result from part (a):

sin 30° = 3sin θ - 4sin³ θ.

Substituting $sin θ = \frac{\sqrt{3}}{4}$ into the equation gives:

sin 30° = 3 \left(\frac{\sqrt{3}}{4}\right) - 4 \left(\frac{\sqrt{3}}{4}\right)^3.

Calculating each term:

First term:

$3 \left(\frac{\sqrt{3}}{4}\right) = \frac{3\sqrt{3}}{4}.$

Second term:

$\left(\frac{\sqrt{3}}{4}\right)^3 = \frac{3\sqrt{3}}{64},$

so:

$-4 \left(\frac{3\sqrt{3}}{64}\right) = -\frac{12\sqrt{3}}{64} = -\frac{3\sqrt{3}}{16}.$

Combining these results gives:

$\sin 30° = \frac{3\sqrt{3}}{4} - \frac{3\sqrt{3}}{16} = \frac{12\sqrt{3}}{16} - \frac{3\sqrt{3}}{16} = \frac{9\sqrt{3}}{16}.$

Thus, the exact value of sin 30° is:

$\sin 30° = \frac{9\sqrt{3}}{16}.$

1. (a) By writing sin 30° as sin(2θ + θ), show that sin 30° = 3sin θ − 4sin³ θ - Edexcel - A-Level Maths Pure - Question 1 - 2007 - Paper 6

Worked Solution & Example Answer:1. (a) By writing sin 30° as sin(2θ + θ), show that sin 30° = 3sin θ − 4sin³ θ - Edexcel - A-Level Maths Pure - Question 1 - 2007 - Paper 6

By writing sin 30° as sin(2θ + θ), show that sin 30° = 3sin θ − 4sin³ θ.

Given that sin θ = \frac{\sqrt{3}}{4}, find the exact value of sin 30°.

Join the A-Level students using SimpleStudy...