Photo AI
Figure 3 shows a sketch of part of the curve with equation y = 7x^2(5 - 2 \sqrt{x}), where x > 0 The curve has a turning point at the point A, where x > 0, as shown in Figure 3 - Edexcel - A-Level Maths Pure - Question 1 - 2018 - Paper 4
Question 1
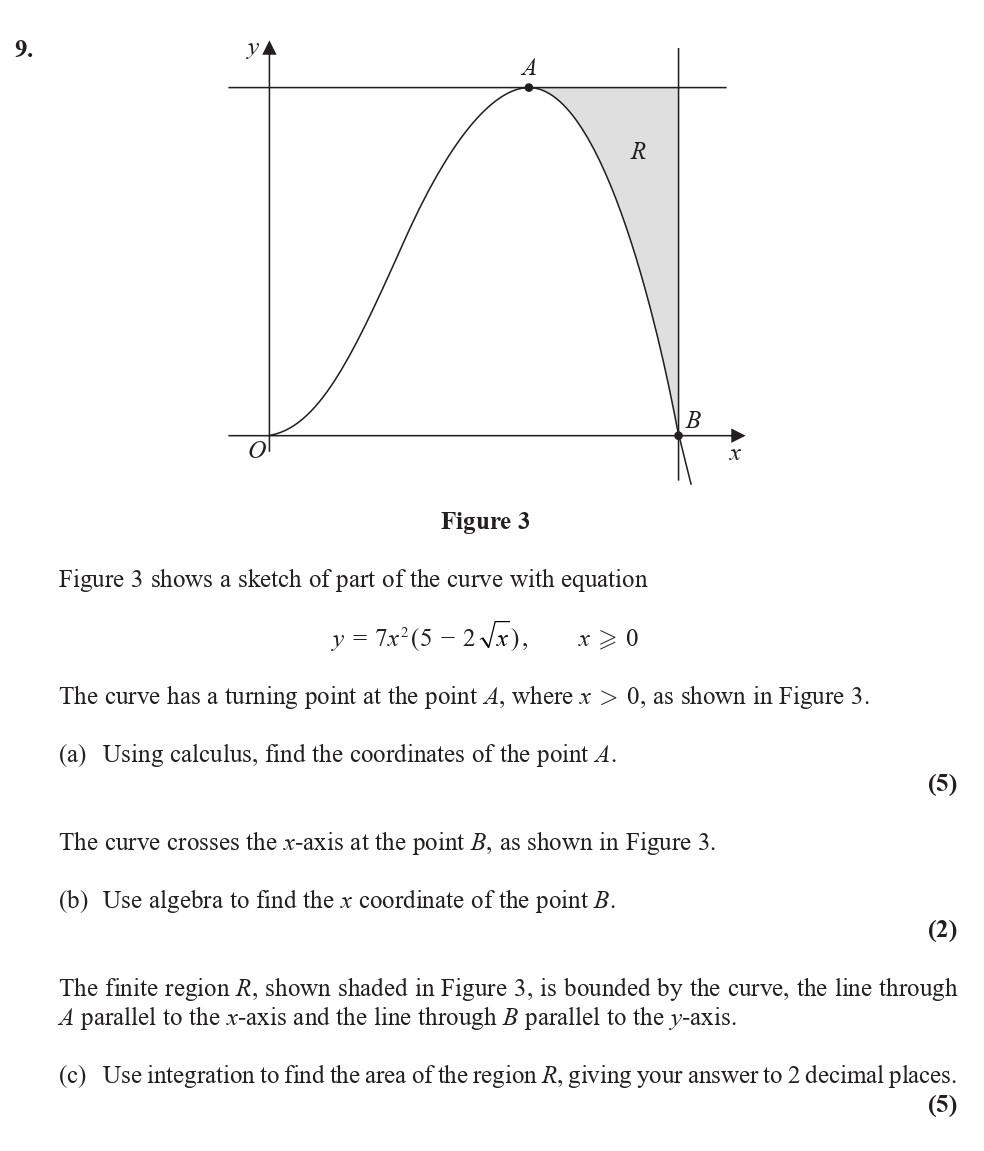
Figure 3 shows a sketch of part of the curve with equation y = 7x^2(5 - 2 \sqrt{x}), where x > 0 The curve has a turning point at the point A, where x > 0, as show... show full transcript
Worked Solution & Example Answer:Figure 3 shows a sketch of part of the curve with equation y = 7x^2(5 - 2 \sqrt{x}), where x > 0 The curve has a turning point at the point A, where x > 0, as shown in Figure 3 - Edexcel - A-Level Maths Pure - Question 1 - 2018 - Paper 4
Step 1
Using calculus, find the coordinates of the point A.
Answer
To find the coordinates of point A, we first need to derive the function. Starting with the equation:
y = 7x^2(5 - 2 \sqrt{x})
We can differentiate y with respect to x:
To find the turning points, we set the derivative equal to zero:
Factoring out 35 gives us:
Thus, either 35 = 0 (which is not possible) or:
Rearranging this gives:
Squaring both sides results in:
We plug back into the original equation to find y:
Thus, the coordinates of point A are (4, 112).
Step 2
Use algebra to find the x coordinate of the point B.
Answer
The curve crosses the x-axis at point B when y = 0. Starting from:
y = 7x^2(5 - 2 \sqrt{x})
Setting this equal to zero gives:
This results in two possibilities: either or:
From the second equation, solving for \sqrt{x} leads to:
Squaring both sides yields:
Thus, the x-coordinate of point B is 6.25.
Step 3
Use integration to find the area of the region R, giving your answer to 2 decimal places.
Answer
To find the area of region R, we use integration between the x-coordinates of points A and B. The area A can be calculated as follows:
Carrying out the integration:
- First, we can simplify the equation and integrate:
- This integral results in:
- Evaluating this between the limits gives us:
- First evaluate at :
- Then evaluate at :
- Subtract to find the area:
Finally, compute these values. The final answer when evaluated will yield:
Thus, the area of the region R is approximately 172.23 square units.
