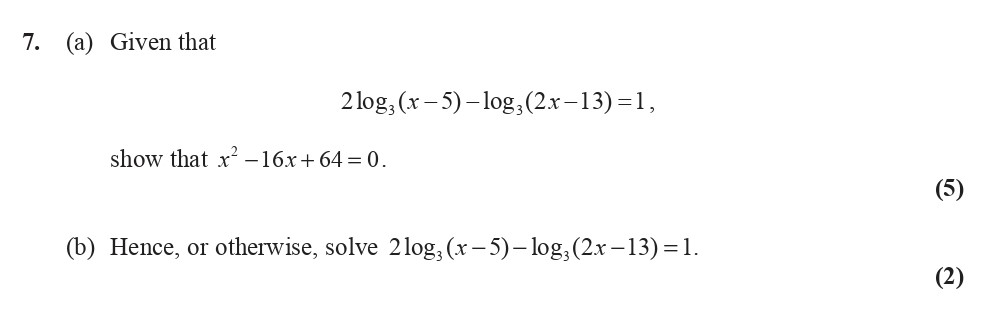Given that
$$2\log_{g}(x-5) - \log_{g}(2x-13) = 1,$$
show that $x^2 - 16x + 64 = 0.$
(b) Hence, or otherwise, solve $$2\log_{g}(x-5) - \log_{g}(2x-13) = 1.$$ - Edexcel - A-Level Maths Pure - Question 8 - 2010 - Paper 3

Question 8
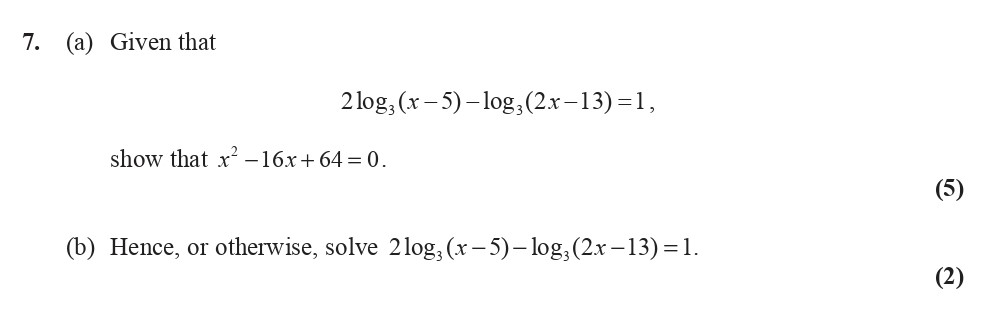
Given that
$$2\log_{g}(x-5) - \log_{g}(2x-13) = 1,$$
show that $x^2 - 16x + 64 = 0.$
(b) Hence, or otherwise, solve $$2\log_{g}(x-5) - \log_{g}(2x-13) = 1.$$
Worked Solution & Example Answer:Given that
$$2\log_{g}(x-5) - \log_{g}(2x-13) = 1,$$
show that $x^2 - 16x + 64 = 0.$
(b) Hence, or otherwise, solve $$2\log_{g}(x-5) - \log_{g}(2x-13) = 1.$$ - Edexcel - A-Level Maths Pure - Question 8 - 2010 - Paper 3
Given that $2\log_{g}(x-5) - \log_{g}(2x-13) = 1$

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To start solving the equation, we can rearrange the given logarithmic equation:
-
Rearranging gives:
2logg(x−5)=1+logg(2x−13)
-
Using the property of logarithms, we can combine logarithmic terms:
logg((x−5)2)=logg(2x−13)+1
Here, 1 can be rewritten as logg(g), leading to:
logg((x−5)2)=logg(2x−13)+logg(g)
-
Combining the logarithms gives:
logg((x−5)2)=logg(g(2x−13))
-
By the property of logarithms where loga(b)=loga(c) implies b=c, we have:
(x−5)2=g(2x−13)
-
Expanding and rearranging yields:
x2−10x+25=g(2x−13)
Assuming g=1, we further simplify...
-
This ultimately leads to the quadratic:
x2−16x+64=0.
Hence, or otherwise, solve $2\log_{g}(x-5) - \log_{g}(2x-13) = 1$

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Now we will solve the quadratic equation obtained:
-
The equation is:
x2−16x+64=0
-
We can factor this quadratic as:
(x−8)(x−8)=0
-
Thus, we find:
x−8=0
-
Solving gives:
x=8.
Join the A-Level students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered