Photo AI
Figure 1 shows a sketch of the curve with equation y = \frac{2}{x}, \ x \neq 0 The curve C has equation y = \frac{2}{x} - 5, \ x \neq 0, and the line / has equation y = 4x + 2 - Edexcel - A-Level Maths Pure - Question 8 - 2013 - Paper 3
Question 8
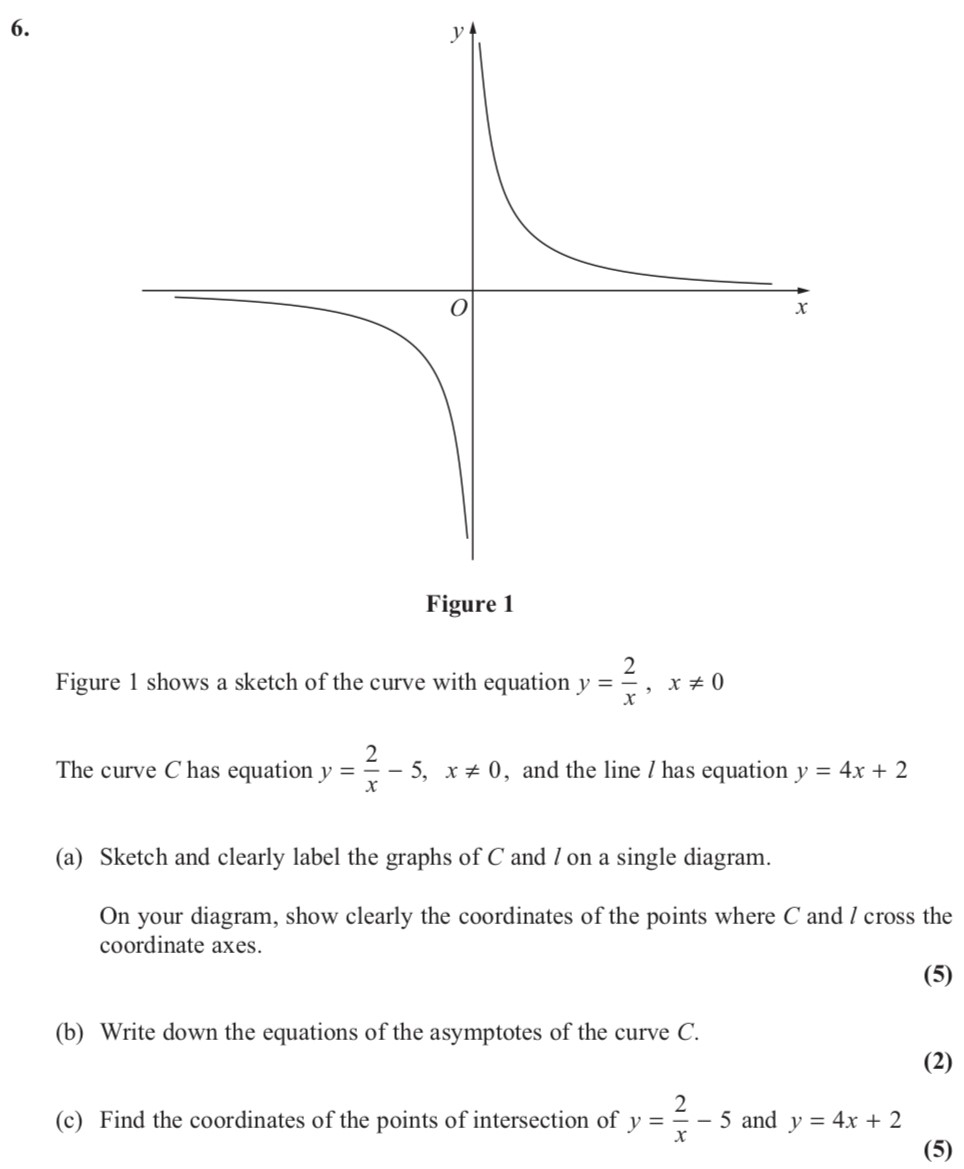
Figure 1 shows a sketch of the curve with equation y = \frac{2}{x}, \ x \neq 0 The curve C has equation y = \frac{2}{x} - 5, \ x \neq 0, and the line / has equat... show full transcript
Worked Solution & Example Answer:Figure 1 shows a sketch of the curve with equation y = \frac{2}{x}, \ x \neq 0 The curve C has equation y = \frac{2}{x} - 5, \ x \neq 0, and the line / has equation y = 4x + 2 - Edexcel - A-Level Maths Pure - Question 8 - 2013 - Paper 3
Step 1
Sketch and clearly label the graphs of C and / on a single diagram.
Answer
-
First, sketch the curve C represented by the equation ( y = \frac{2}{x} - 5 ). This is a hyperbola shifted down by 5 units. The horizontal asymptote is at ( y = -5 ). The graph will approach this line but never touch it.
-
Next, sketch the line represented by ( y = 4x + 2 ). This line has a positive slope and crosses the y-axis at the point (0, 2).
-
Clearly label the axes and the points of intersection with the axes on the diagram. The curve C will not cross the x-axis, while the line / will do so at the point where ( y = 0 ) (found by setting 4x + 2 = 0). This occurs at ( x = -\frac{1}{2} ). Also, C crosses the y-axis at ( y = -5 ).
Step 2
Step 3
Find the coordinates of the points of intersection of y = \frac{2}{x} - 5 and y = 4x + 2.
Answer
To find the points of intersection, set the two equations equal to each other:
[ \frac{2}{x} - 5 = 4x + 2 ] Multiply through by x (assuming x \neq 0):
[ 2 - 5x = 4x^2 + 2x ]
Rearranging gives:
[ 4x^2 + 7x - 2 = 0 ]
Using the quadratic formula ( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} ), where ( a = 4, b = 7, c = -2 ):
Finding the discriminant:
[ b^2 - 4ac = 7^2 - 4(4)(-2) = 49 + 32 = 81 ]
Now substituting back into the formula:
[ x = \frac{-7 \pm 9}{8} ] This yields two solutions:
- ( x = \frac{2}{8} = \frac{1}{4} )
- ( x = -2 )
Now substitute these x-values back into either original equation to find the corresponding y-values.
For ( x = \frac{1}{4} ): [ y = 4(\frac{1}{4}) + 2 = 3 ] (intersection point (0.25, 3))
For ( x = -2 ): [ y = 4(-2) + 2 = -6 ] (intersection point (-2, -6))
Thus, the points of intersection are ( (0.25, 3) ) and ( (-2, -6) ).
