Photo AI
The curve C has the equation $$\cos 2x + \cos 3y = 1,$$ where $-\frac{\pi}{4} \leq x \leq \frac{\pi}{4}$ and $0 \leq y < \frac{\pi}{6}$ - Edexcel - A-Level Maths Pure - Question 3 - 2010 - Paper 7
Question 3
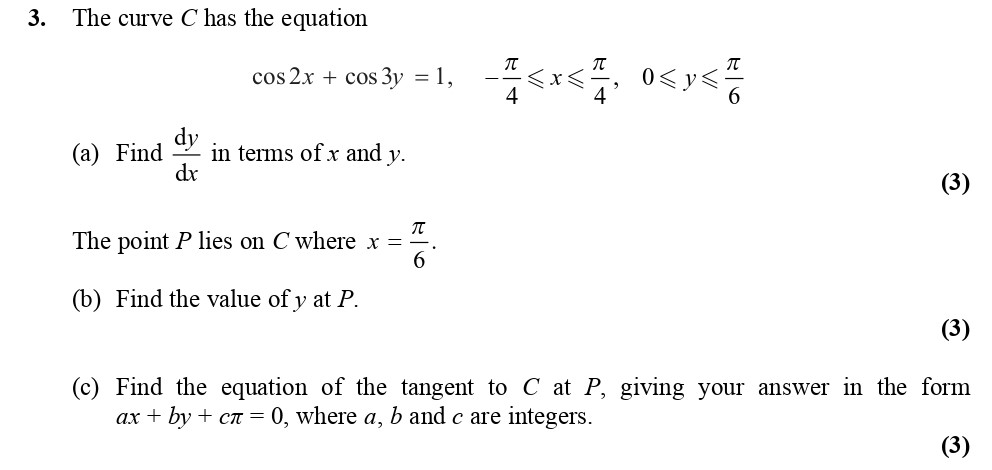
The curve C has the equation $$\cos 2x + \cos 3y = 1,$$ where $-\frac{\pi}{4} \leq x \leq \frac{\pi}{4}$ and $0 \leq y < \frac{\pi}{6}$. (a) Find $\frac{dy}{dx}$ ... show full transcript
Worked Solution & Example Answer:The curve C has the equation $$\cos 2x + \cos 3y = 1,$$ where $-\frac{\pi}{4} \leq x \leq \frac{\pi}{4}$ and $0 \leq y < \frac{\pi}{6}$ - Edexcel - A-Level Maths Pure - Question 3 - 2010 - Paper 7
Step 1
Step 2
Step 3
Find the equation of the tangent to C at P, giving your answer in the form ax + by + cπ = 0.
Answer
To find the equation of the tangent at P, we first evaluate using the value of :
The slope of the tangent line at point P (where , ) can be expressed as:
where and .
Substituting these values gives:
Rearranging this yields:
By calculating b, we can express the tangent equation in the necessary form. After rearranging, we find the form becomes:
which corresponds to integers a, b, and c.
