Photo AI
Given the function: $$f(x) = x^3 + 3x^2 + 5.$$ Find (a) $f''(x)$, (b) $\int_{1}^{2} f(x) \, dx$. - Edexcel - A-Level Maths Pure - Question 3 - 2007 - Paper 2
Question 3
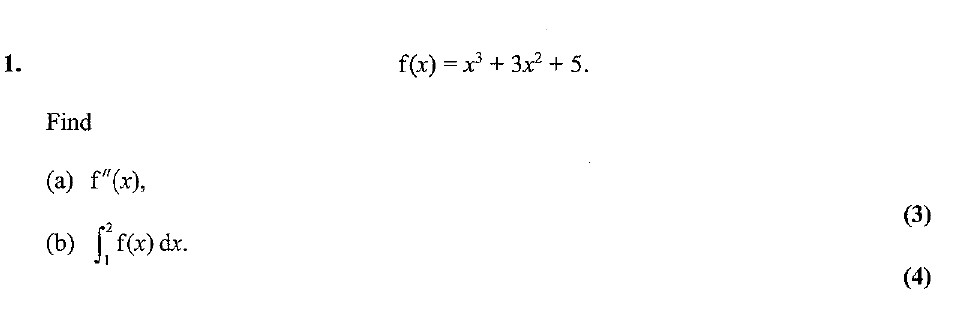
Given the function: $$f(x) = x^3 + 3x^2 + 5.$$ Find (a) $f''(x)$, (b) $\int_{1}^{2} f(x) \, dx$.
Worked Solution & Example Answer:Given the function: $$f(x) = x^3 + 3x^2 + 5.$$ Find (a) $f''(x)$, (b) $\int_{1}^{2} f(x) \, dx$. - Edexcel - A-Level Maths Pure - Question 3 - 2007 - Paper 2
Step 1
Step 2
(b) $\int_{1}^{2} f(x) \, dx$
Answer
To solve the integral , we substitute into the integral:
This breaks down into three separate integrals:
Calculating each integral:
-
For , we have: evaluated from 1 to 2 gives:
-
For , we have: evaluated from 1 to 2 gives:
-
For , we have: evaluated from 1 to 2 gives:
Now, summing these results together:
Thus, the final answer is:
