Photo AI
Figure 3 shows the shaded region R which is bounded by the curve $y = -2x^2 + 4x$ and the line $y = \frac{3}{2}$ - Edexcel - A-Level Maths Pure - Question 2 - 2005 - Paper 2
Question 2
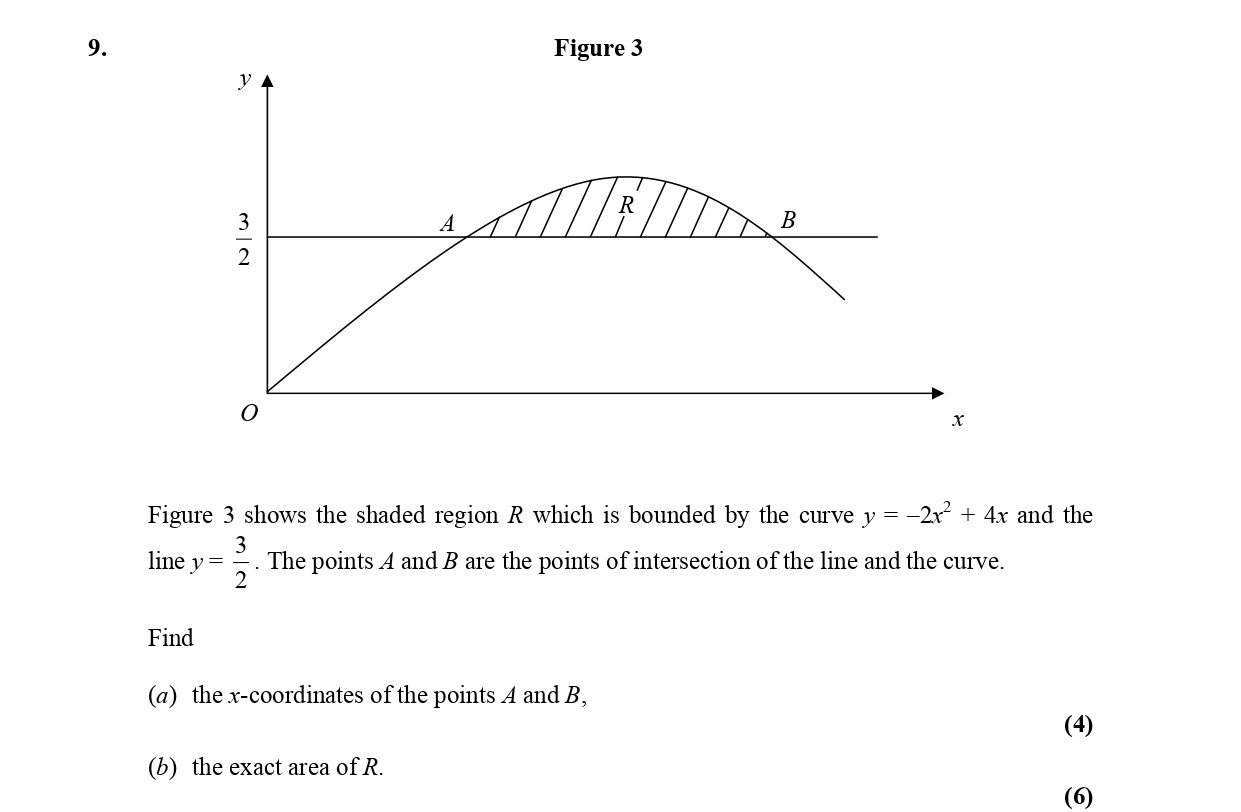
Figure 3 shows the shaded region R which is bounded by the curve $y = -2x^2 + 4x$ and the line $y = \frac{3}{2}$. The points A and B are the points of intersection o... show full transcript
Worked Solution & Example Answer:Figure 3 shows the shaded region R which is bounded by the curve $y = -2x^2 + 4x$ and the line $y = \frac{3}{2}$ - Edexcel - A-Level Maths Pure - Question 2 - 2005 - Paper 2
Step 1
(a) the x-coordinates of the points A and B
Answer
To find the x-coordinates of points A and B, we need to determine where the line intersects the curve:
Set the equations equal:
Rearranging gives:
Multiplying through by -1 to simplify:
Next, multiply the entire equation by 2 to eliminate the fraction:
Now we will apply the quadratic formula, where , , and :
Calculating the discriminant:
Thus:
Solving this gives the x-coordinates:
Therefore, the x-coordinates of points A and B are and .
Step 2
(b) the exact area of R
Answer
To find the area of the region R between the curve and the line, we will integrate the difference of the functions from x = \frac{1}{2}x = \frac{3}{2}$:
Simplifying the integrand:
Now, we separate the integral:
Evaluating each integral:
Calculating:
So the area becomes:
Clearly an algebraic mistake earlier, let’s ensure by performing calculations again for each integral and consolidating:
Thus, the exact area is: .
