Photo AI
Figure 1 shows a sketch of the curve C with equation y = \frac{4x^{2} + x}{2\sqrt{x}} \quad x > 0 (a) Show that \frac{dy}{dx} = \frac{12x^{2} + x - 16\sqrt{x}}{4\sqrt{x}} The point P, shown in Figure 1, is the minimum turning point on C - Edexcel - A-Level Maths Pure - Question 9 - 2020 - Paper 2
Question 9
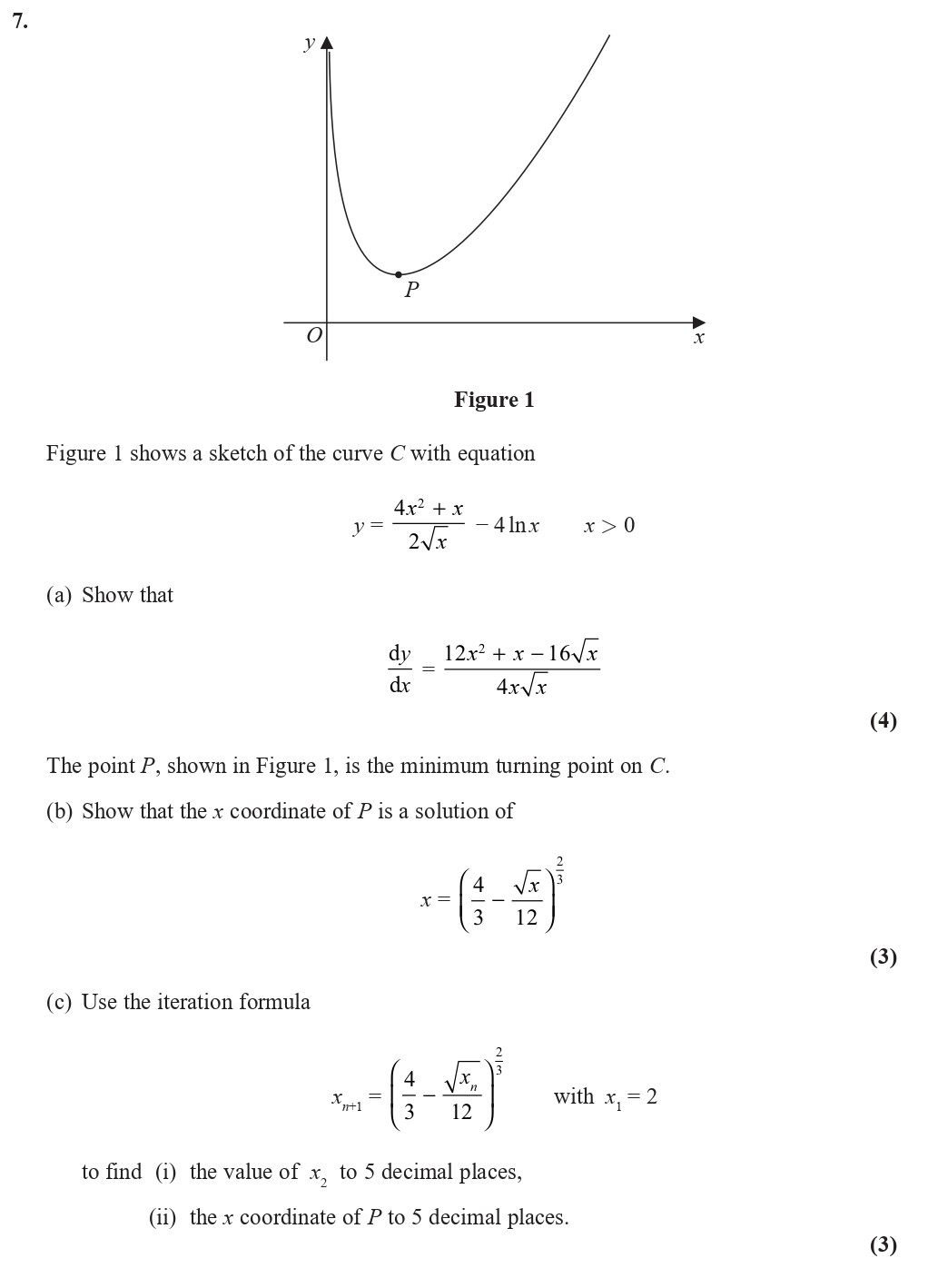
Figure 1 shows a sketch of the curve C with equation y = \frac{4x^{2} + x}{2\sqrt{x}} \quad x > 0 (a) Show that \frac{dy}{dx} = \frac{12x^{2} + x - 16\sqrt{x}}{4\... show full transcript
Worked Solution & Example Answer:Figure 1 shows a sketch of the curve C with equation y = \frac{4x^{2} + x}{2\sqrt{x}} \quad x > 0 (a) Show that \frac{dy}{dx} = \frac{12x^{2} + x - 16\sqrt{x}}{4\sqrt{x}} The point P, shown in Figure 1, is the minimum turning point on C - Edexcel - A-Level Maths Pure - Question 9 - 2020 - Paper 2
Step 1
Show that \( \frac{dy}{dx} = \frac{12x^{2} + x - 16\sqrt{x}}{4\sqrt{x}} \)
Answer
To find the derivative of the function ( y = \frac{4x^{2} + x}{2\sqrt{x}} ), we will use the quotient rule, which states that if ( f(x) = \frac{g(x)}{h(x)} ), then ( f'(x) = \frac{g'(x)h(x) - g(x)h'(x)}{(h(x))^2} ).
Let ( g(x) = 4x^{2} + x ) and ( h(x) = 2\sqrt{x} ).
Calculating the derivatives:
- ( g'(x) = 8x + 1 )
- ( h'(x) = \frac{1}{\sqrt{x}} ) (using the power rule on ( h(x) = 2x^{\frac{1}{2}} ))
Substituting these into the quotient rule gives:
Simplifying the numerator:
- The first term: ( (8x + 1)(2\sqrt{x}) = 16x\sqrt{x} + 2\sqrt{x} )
- The second term: ( \frac{4x^{2} + x}{\sqrt{x}} = 4x^{\frac{3}{2}} + x^{\frac{1}{2}} )
Putting these together:
Collecting the like terms in the numerator leads to the expression:
Step 2
Show that the x coordinate of P is a solution of \( x = \left(\frac{4 - \sqrt{12}}{3}\right)^{\frac{3}{2}} \)
Answer
To find the x-coordinate of the minimum turning point P, we need to set ( \frac{dy}{dx} = 0 ).
Setting the numerator to zero:
Letting ( u = \sqrt{x} ), then we rewrite the equation as:
Factoring out a common term:
We discard ( u = 0 ) for ( x > 0 ). Now we can solve ( 12u^{3} + u - 16 = 0 ).
Using the Rational Root Theorem and synthetic division, we can find one solution, and from there use numerical methods to find the approximate value:
After solving, the x-coordinate simplifies to:
( x = \left(\frac{4 - \sqrt{12}}{3}\right)^{\frac{3}{2}} ).
Step 3
(ii) the x coordinate of P to 5 decimal places
Answer
Continuing the iteration to find ( x_{3} ):
Using ( x_{2} \approx 0.1974 ):
This computation provides an x-coordinate value closer to the actual minimum point P.
Repeating the iterations may give us: ( x_{3} \approx 1.16560 ) (to 5 decimal places).
Ensure to round appropriately to get the final result.
