Photo AI
7. (a) Prove that $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} + \frac{\sin \theta}{\sin \theta} = 2 \csc 2\theta, \quad \theta \neq 90^\circ.$$ (b) On the axes on page 20, sketch the graph of $$y = 2 \csc 2\theta$$ for $$0^\circ < \theta < 360^\circ.$$ (c) Solve, for $$0^\circ < \theta < 360^\circ$$, the equation $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} \cdot \frac{\sin \theta}{\sin \theta} = 3,$$ giving your answers to 1 decimal place. - Edexcel - A-Level Maths Pure - Question 1 - 2007 - Paper 5
Question 1
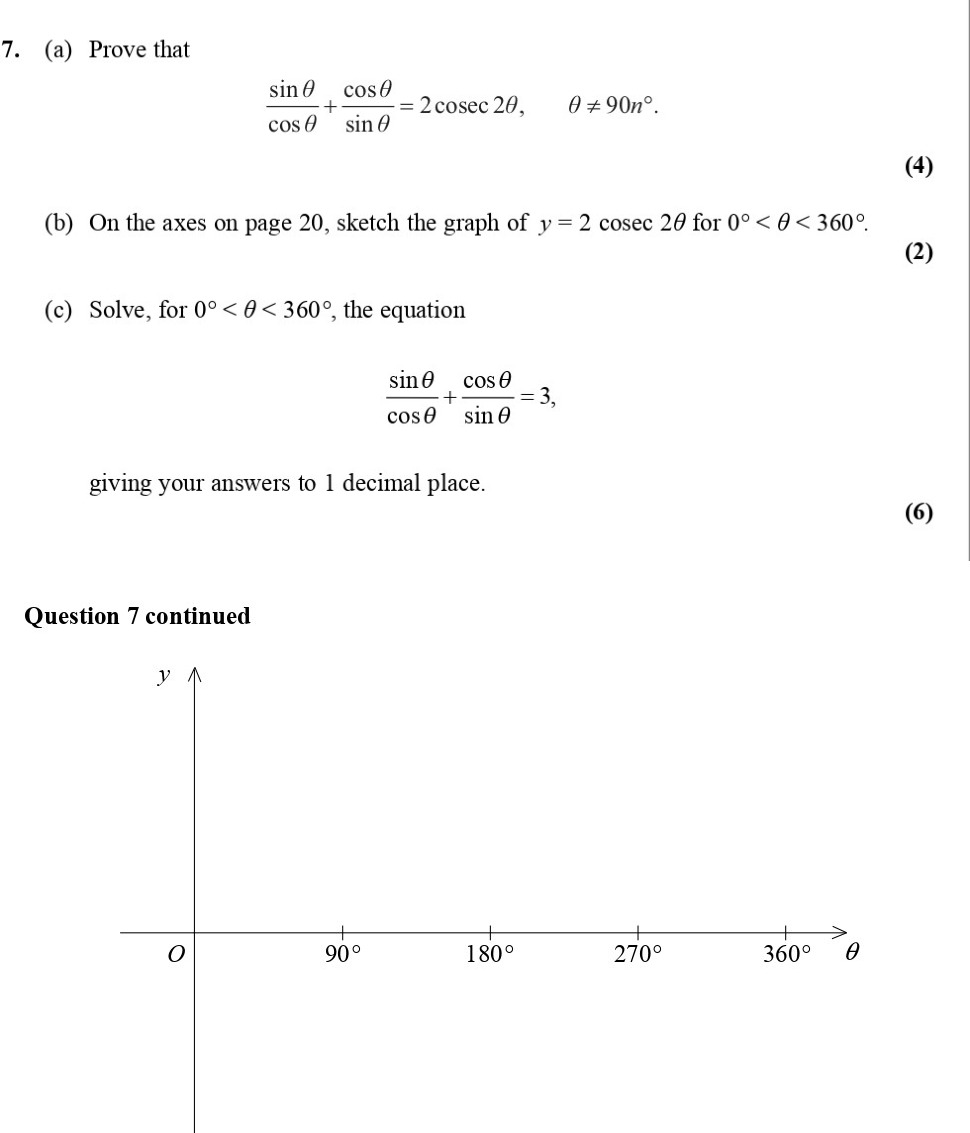
7. (a) Prove that $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} + \frac{\sin \theta}{\sin \theta} = 2 \csc 2\theta, \quad \theta \neq 90^\circ.$$ (b) On... show full transcript
Worked Solution & Example Answer:7. (a) Prove that $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} + \frac{\sin \theta}{\sin \theta} = 2 \csc 2\theta, \quad \theta \neq 90^\circ.$$ (b) On the axes on page 20, sketch the graph of $$y = 2 \csc 2\theta$$ for $$0^\circ < \theta < 360^\circ.$$ (c) Solve, for $$0^\circ < \theta < 360^\circ$$, the equation $$\frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} \cdot \frac{\sin \theta}{\sin \theta} = 3,$$ giving your answers to 1 decimal place. - Edexcel - A-Level Maths Pure - Question 1 - 2007 - Paper 5
Step 1
Prove that \( \frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} + \frac{\sin \theta}{\sin \theta} = 2 \csc 2\theta \)
Answer
To prove the identity, we'll start by simplifying the left-hand side:
-
Combine the fractions onto a common denominator:
-
Notice that we can express the numerator as:
-
Use the double angle sine identity:
Thus, our expression becomes: .
This proves the identity correctly.
Step 2
On the axes on page 20, sketch the graph of \( y = 2 \csc 2\theta \) for \( 0^\circ < \theta < 360^\circ \)
Answer
To sketch the graph of ( y = 2 \csc 2\theta ):
-
Identify vertical asymptotes: The function ( \csc , \theta ) is undefined where ( \sin 2\theta = 0 ). This occurs at: Hence, the vertical asymptotes are at ( \theta = 0^\circ, 90^\circ, 180^\circ, 270^\circ, 360^\circ ).
-
Determine values of the function: The maximum and minimum points of the function occur when ( \sin 2\theta = 1 ) and ( \sin 2\theta = -1 ), giving maximum and minimum values of 2 and -2 respectively.
-
Sketch the graph: Plot the points, asymptotes, and minimum/maximum values to create a repeated wave pattern with the specified range.
Step 3
Solve, for \( 0^\circ < \theta < 360^\circ \), the equation \( \frac{\sin \theta \cdot \cos \theta}{\cos^2 \theta} \cdot \frac{\sin \theta}{\sin \theta} = 3 \)
Answer
To solve the equation:
-
The given equation simplifies to:
-
Use the identity ( \sin^2 \theta + \cos^2 \theta = 1 ): Substitute ( \sin^2 \theta = 3(1 - \sin^2 \theta) ) leading to:
-
Find angles: Using the principal values for ( \sin \theta = \frac{\sqrt{3}}{2} ) gives:
- ( \theta = 60^\circ )
- ( \theta = 120^\circ ) and for ( \sin \theta = -\frac{\sqrt{3}}{2} ):
- ( \theta = 240^\circ )
- ( \theta = 300^\circ )
Thus, the solutions in the range are approximately:
- ( \theta = 60.0^\circ, 120.0^\circ, 240.0^\circ, 300.0^\circ )
