Photo AI
A curve C has equation y = \frac{3}{(5-3x)^2}, \quad x \neq \frac{5}{3} The point P on C has x-coordinate 2 - Edexcel - A-Level Maths Pure - Question 4 - 2010 - Paper 5
Question 4
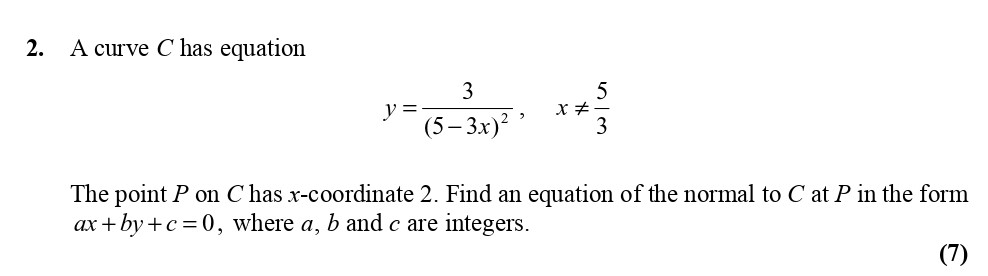
A curve C has equation y = \frac{3}{(5-3x)^2}, \quad x \neq \frac{5}{3} The point P on C has x-coordinate 2. Find an equation of the normal to C at P in the form a... show full transcript
Worked Solution & Example Answer:A curve C has equation y = \frac{3}{(5-3x)^2}, \quad x \neq \frac{5}{3} The point P on C has x-coordinate 2 - Edexcel - A-Level Maths Pure - Question 4 - 2010 - Paper 5
Step 1
Step 2
Step 3
Step 4
Use point-slope form to find the equation of the normal
Answer
Using the point-slope form of the equation:
we substitute the coordinates of P (2, 3):
Multiplying through by 18 to eliminate the fraction results in:
This simplifies to:
Thus, the equation in the required form ax + by + c = 0 is:
with a = 1, b = -18, and c = 56.
