Photo AI
Figure 2 shows a sketch of the graph with equation $$y = 2|x + 4| - 5$$ The vertex of the graph is at the point P, shown in Figure 2 - Edexcel - A-Level Maths Pure - Question 13 - 2020 - Paper 2
Question 13
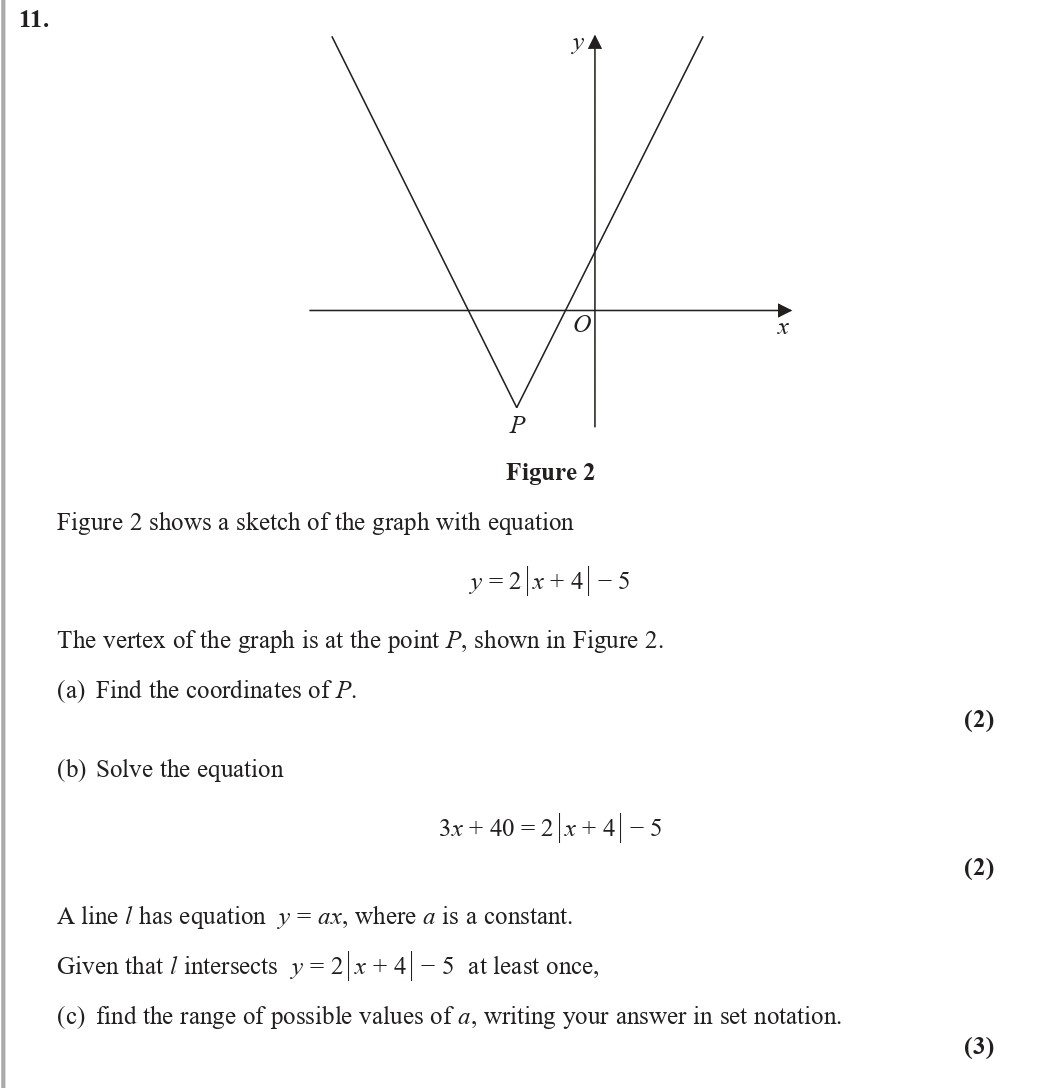
Figure 2 shows a sketch of the graph with equation $$y = 2|x + 4| - 5$$ The vertex of the graph is at the point P, shown in Figure 2. (a) Find the coordinates of ... show full transcript
Worked Solution & Example Answer:Figure 2 shows a sketch of the graph with equation $$y = 2|x + 4| - 5$$ The vertex of the graph is at the point P, shown in Figure 2 - Edexcel - A-Level Maths Pure - Question 13 - 2020 - Paper 2
Step 1
Find the coordinates of P.
Answer
To find the coordinates of point P, we look at the equation of the graph, which is given by
.
The vertex occurs where the expression inside the absolute value is zero. Setting
,
we find that
.
Now, substituting this value back into the equation to find y:
Thus, the coordinates of P are
.
Step 2
Solve the equation 3x + 40 = 2|x + 4| - 5.
Answer
To solve the equation
we first simplify the right side:
Next, we can isolate the absolute value:
We will solve this by considering two cases for the absolute value.
Case 1: x + 4 ≥ 0
In this case,
.
Multiplying through by 2:
Case 2: x + 4 < 0
Here,
Multiplying through by 2:
Thus, the two solutions are:
Step 3
find the range of possible values of a, writing your answer in set notation.
Answer
To find the range of possible values of a, we consider when the line
intersects the given graph. For intersections to occur, the slope a must ensure that the line can touch or cross the V-shaped graph. Since the vertex is downward at P(-4, -5), the intersection occurs when
Thus, the range of values for a in set notation is:
