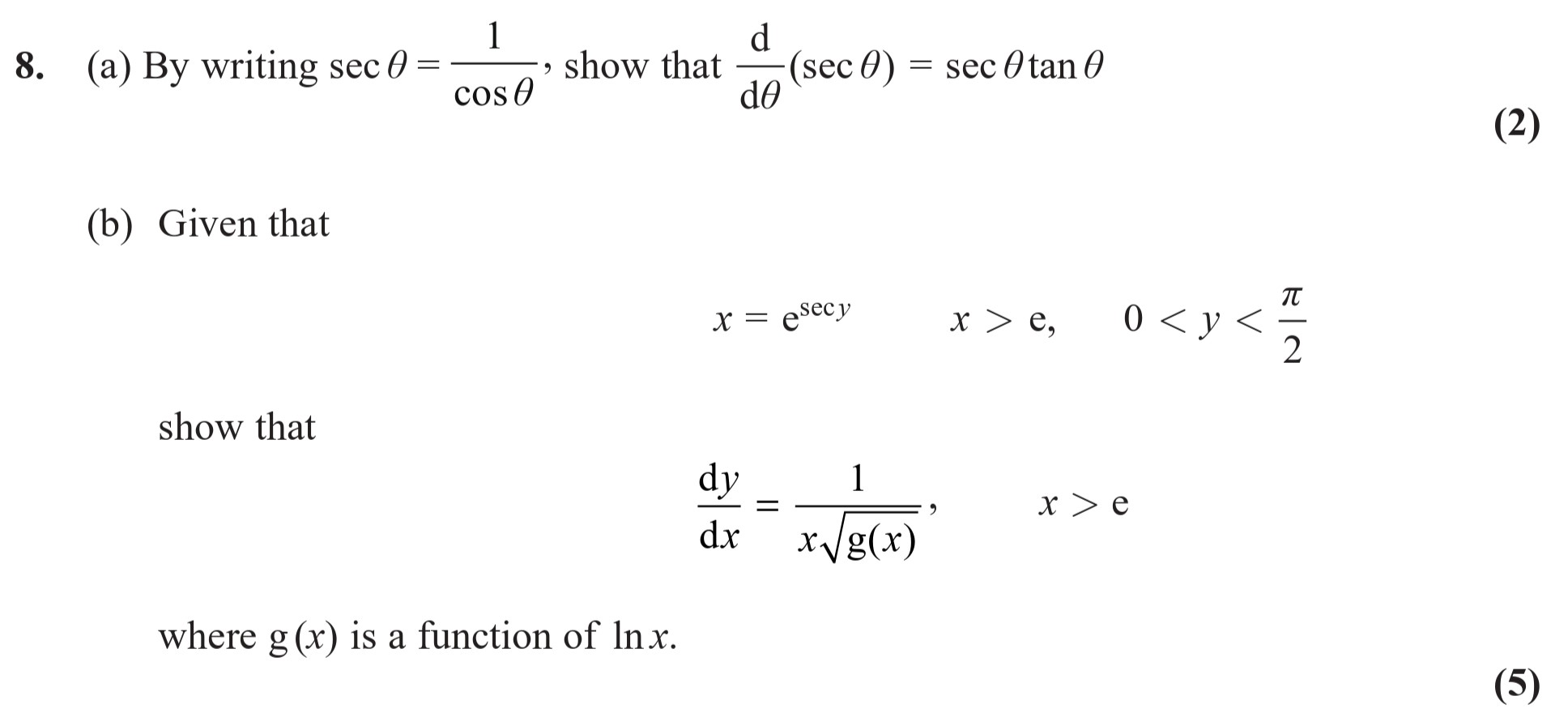
8. (a) By writing sec θ = \frac{1}{cos θ}, show that \frac{d}{dθ}(sec θ) = sec θtan θ (b) Given that x = e^{sec y}, x > e, \, 0 < y < \frac{π}{2} show that \frac{dy}{dx} = \frac{1}{x \, g(x)} \, \, x > e where g(x) is a function of ln x. - Edexcel - A-Level Maths Pure - Question 8 - 2018 - Paper 5

Starting with the relationship (x = e^{sec y}), we differentiate both sides with respect to x.

Since the left hand side is simply 1 (as it derives itself):

dx/dx = 1

On the right hand side:

dy/dx \cdot e^{sec y} \cdot sec y , tan y\ \text{(chain rule)}

Equating these gives us:

$1 = \frac{dy}{dx} \cdot e^{sec y} \cdot sec y \cdot tan y$

Now, we can rewrite this to isolate \frac{dy}{dx}:

$\frac{dy}{dx} = \frac{1}{e^{sec y} \cdot sec y \cdot tan y}$

Since (x = e^{sec y}) then we can write:

$= \frac{1}{x \cdot sec y \cdot tan y}$

Next, noticing that sec y can be expressed in terms of ln x:

let (g(x) = sec y \cdot tan y), therefore:

$\frac{dy}{dx} = \frac{1}{x \cdot g(x)}$ where g(x) is indeed a function of ln x, completing the solution.