Photo AI
Figure 4 shows a solid brick in the shape of a cuboid measuring $2x$ cm by $x$ cm by $y$ cm - Edexcel - A-Level Maths Pure - Question 3 - 2007 - Paper 2
Question 3
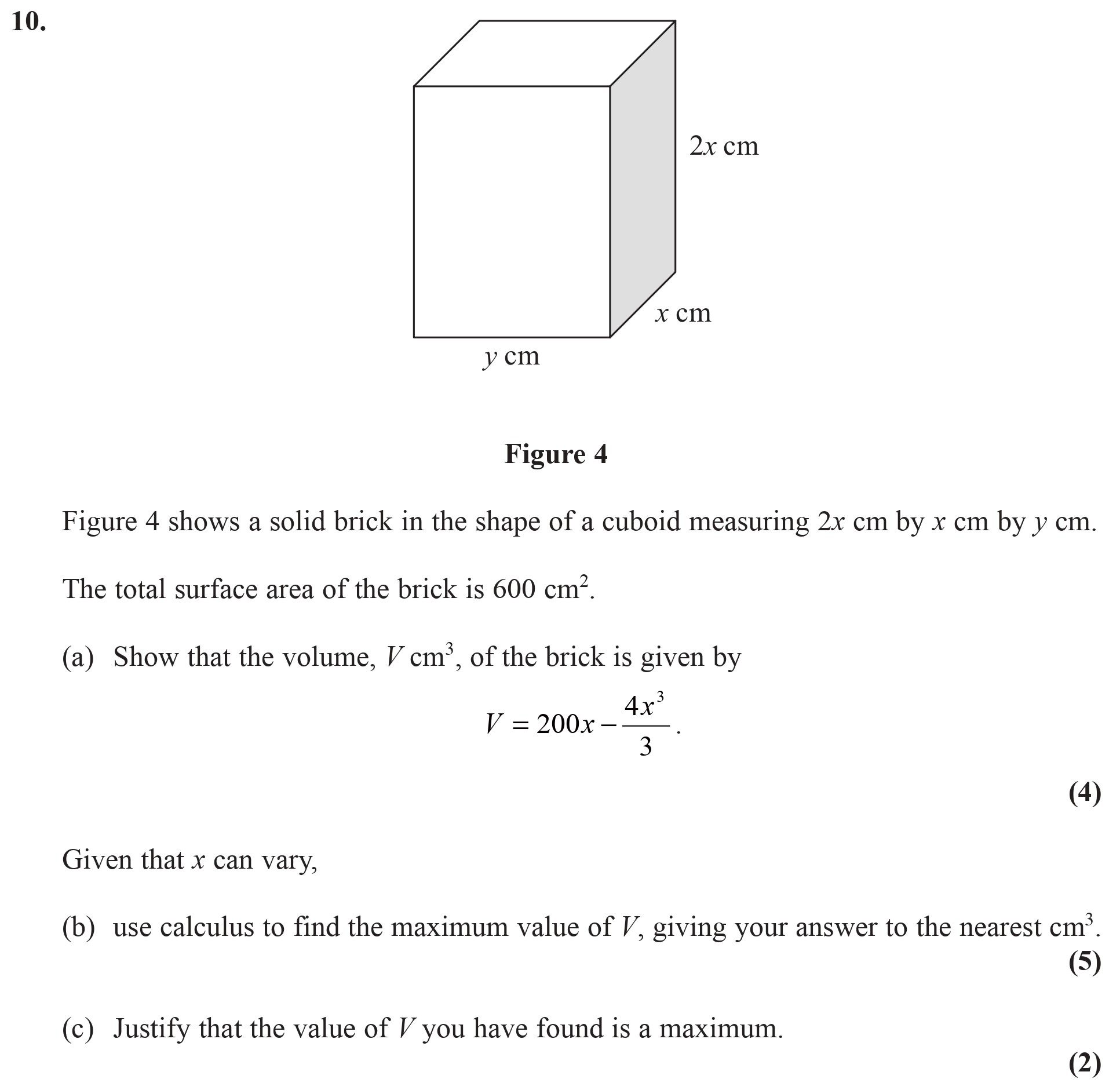
Figure 4 shows a solid brick in the shape of a cuboid measuring $2x$ cm by $x$ cm by $y$ cm. The total surface area of the brick is 600 cm$^2$. (a) Show that the v... show full transcript
Worked Solution & Example Answer:Figure 4 shows a solid brick in the shape of a cuboid measuring $2x$ cm by $x$ cm by $y$ cm - Edexcel - A-Level Maths Pure - Question 3 - 2007 - Paper 2
Step 1
Show that the volume, $V$ cm$^3$, of the brick is given by
Answer
To find the volume of the brick, we start with the given dimensions:
- Length = cm
- Width = cm
- Height = cm
The formula for the total surface area () of a cuboid is:
Substituting the values into the surface area equation gives:
From this, we can express in terms of :
Now, substitute into the volume formula:
Thus, we have shown the volume as required.
Step 2
use calculus to find the maximum value of $V$, giving your answer to the nearest cm$^3$.
Answer
To find the maximum value of , we first need to differentiate with respect to :
We set the derivative to zero to find critical points:
Next, we calculate the volume at this critical point:
Calculating gives:
Now let's evaluate :
Calculating gives approximately cm.
Step 3
Justify that the value of $V$ you have found is a maximum.
Answer
To confirm that the value found is a maximum, we will check the second derivative:
At the critical point :
indicating that the function is concave down at this point. Thus, has a local maximum at this critical point, justifying that the volume we found is indeed a maximum.
