A-Level Edexcel Maths Pure General Binomial Expansion: Figure 3 shows the shaded region

Figure 3 shows the shaded region R which is bounded by the curve $y = -2x^2 + 4x$ and the line $y = \frac{3}{2}$ - Edexcel - A-Level Maths Pure - Question 2 - 2006 - Paper 2

Question 2

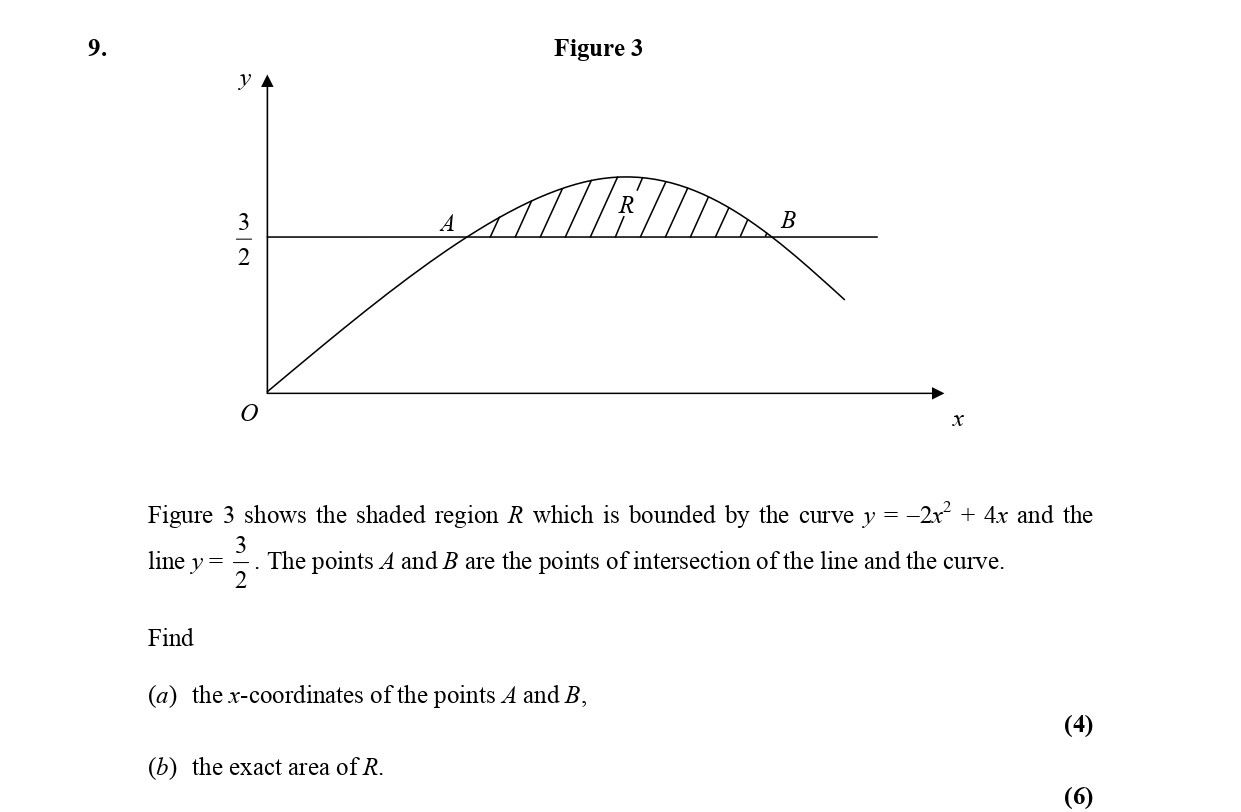
$Figure-3-shows-the-shaded-region-R-which-is-bounded-by-the-curve-$y-=--2x^2-+-4x$-and-the-line-$y-=-\frac{3}{2}$-Edexcel-A-Level Maths Pure-Question 2-2006-Paper 2.png$

Figure 3 shows the shaded region R which is bounded by the curve $y = -2x^2 + 4x$ and the line $y = \frac{3}{2}$. The points A and B are the points of intersection o... show full transcript

Worked Solution & Example Answer:Figure 3 shows the shaded region R which is bounded by the curve $y = -2x^2 + 4x$ and the line $y = \frac{3}{2}$ - Edexcel - A-Level Maths Pure - Question 2 - 2006 - Paper 2

Step 1

(a) the x-coordinates of the points A and B

96%

114 rated

Answer

To find the x-coordinates of the points A and B, we need to set the equation of the curve equal to the equation of the line:

-2x^2 + 4x = \frac{3}{2}

First, rearranging this gives:

-2x^2 + 4x - \frac{3}{2} = 0

Multiplying through by -1 to simplify, we have:

2x^2 - 4x + \frac{3}{2} = 0

Now, multiplying every term by 2 to eliminate the fraction yields:

4x^2 - 8x + 3 = 0

Applying the quadratic formula:

x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

Where $a = 4$ , $b = -8$ , and $c = 3$ :

x = \frac{8 \pm \sqrt{(-8)^2 - 4 \cdot 4 \cdot 3}}{2 \cdot 4} = \frac{8 \pm \sqrt{64 - 48}}{8} = \frac{8 \pm \sqrt{16}}{8} = \frac{8 \pm 4}{8}

Therefore:

x = \frac{12}{8} = \frac{3}{2} \quad ext{or} \quad x = \frac{4}{8} = \frac{1}{2}

The x-coordinates of points A and B are $x = \frac{1}{2}$ and $x = \frac{3}{2}$ , respectively.

Step 2

(b) the exact area of R

99%

104 rated

Answer

To find the area of the shaded region R, we can use the integral of the upper function minus the lower function over the interval from $x = \frac{1}{2}$ to $x = \frac{3}{2}$ :

\text{Area} = \int_{\frac{1}{2}}^{\frac{3}{2}} \left( -2x^2 + 4x - \frac{3}{2} \right) dx

Calculating the integral:

\int (-2x^2 + 4x - \frac{3}{2}) dx = \left[ -\frac{2}{3}x^3 + 2x^2 - \frac{3}{2}x \right]_{\frac{1}{2}}^{\frac{3}{2}}

Now evaluating this from $x = \frac{1}{2}$ to $x = \frac{3}{2}$ :

Evaluating at $x = \frac{3}{2}$ :
- Calculate $\left( -\frac{2}{3}\left(\frac{3}{2}\right)^3 + 2\left(\frac{3}{2}\right)^2 - \frac{3}{2}\left(\frac{3}{2}\right) \right)$
Evaluating at $x = \frac{1}{2}$ :
- Calculate $\left( -\frac{2}{3}\left(\frac{1}{2}\right)^3 + 2\left(\frac{1}{2}\right)^2 - \frac{3}{2}\left(\frac{1}{2}\right) \right)$

Finally, after substituting and performing the calculations, we find that the exact area of R is:

\text{Area} = \frac{11}{6} - \frac{1}{3} = \frac{11}{6} - \frac{2}{6} = \frac{9}{6} = \frac{3}{2}

Figure 3 shows the shaded region R which is bounded by the curve $y = -2x^2 + 4x$ and the line $y = \frac{3}{2}$ - Edexcel - A-Level Maths Pure - Question 2 - 2006 - Paper 2

Worked Solution & Example Answer:Figure 3 shows the shaded region R which is bounded by the curve $y = -2x^2 + 4x$ and the line $y = \frac{3}{2}$ - Edexcel - A-Level Maths Pure - Question 2 - 2006 - Paper 2

(a) the x-coordinates of the points A and B

(b) the exact area of R

Join the A-Level students using SimpleStudy...