Photo AI
The finite region R, as shown in Figure 2, is bounded by the x-axis and the curve with equation $$y = 27 - 2x - 9 rac{16}{x^2}, \quad x > 0$$ The curve crosses the x-axis at the points (1, 0) and (4, 0) - Edexcel - A-Level Maths Pure - Question 1 - 2013 - Paper 6
Question 1
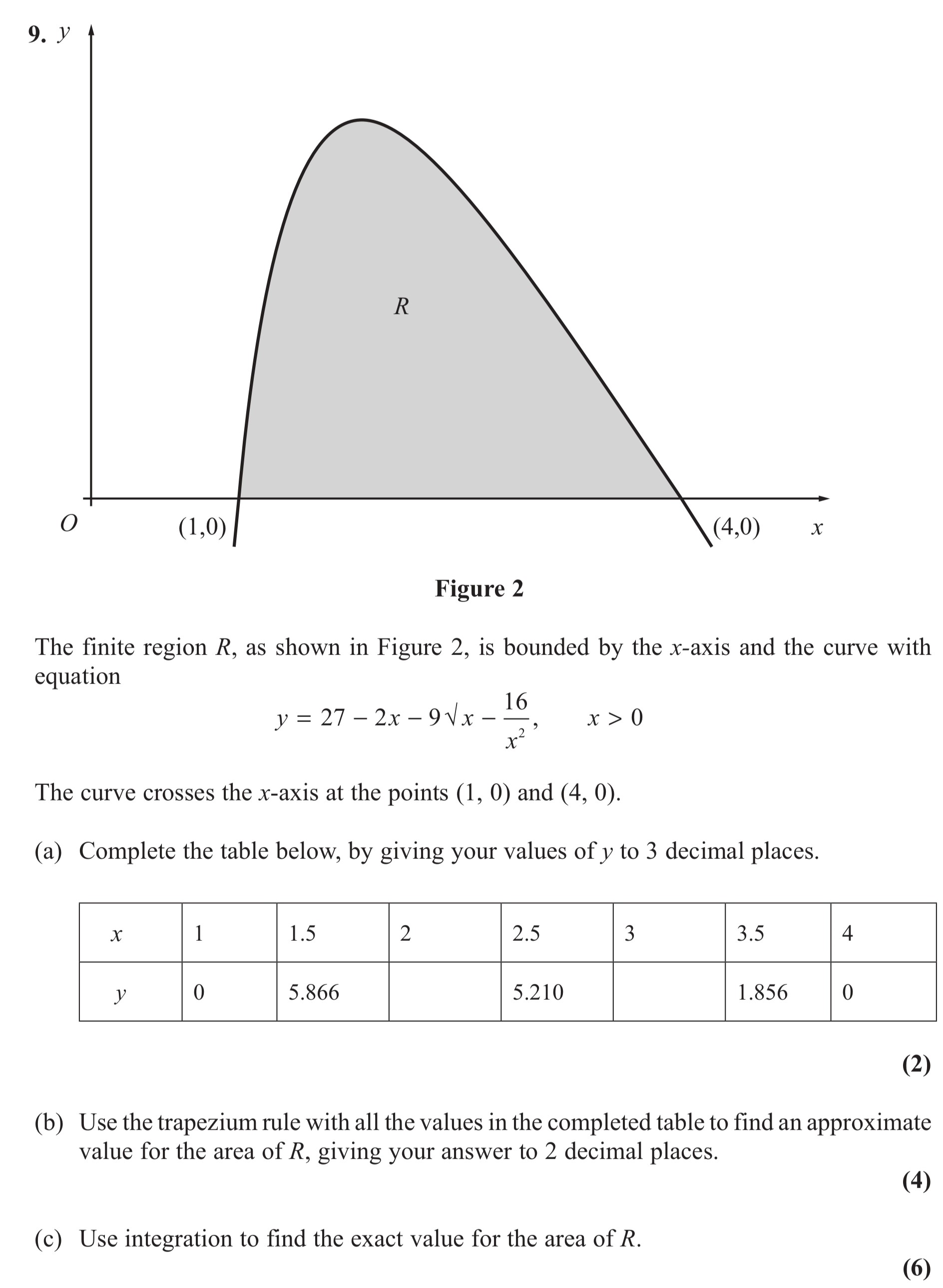
The finite region R, as shown in Figure 2, is bounded by the x-axis and the curve with equation $$y = 27 - 2x - 9 rac{16}{x^2}, \quad x > 0$$ The curve crosses the... show full transcript
Worked Solution & Example Answer:The finite region R, as shown in Figure 2, is bounded by the x-axis and the curve with equation $$y = 27 - 2x - 9 rac{16}{x^2}, \quad x > 0$$ The curve crosses the x-axis at the points (1, 0) and (4, 0) - Edexcel - A-Level Maths Pure - Question 1 - 2013 - Paper 6
Step 1
Complete the table below, by giving your values of y to 3 decimal places.
Answer
To complete the table, we substitute the given x values into the equation.
-
For :
y = 27 - 2(1) - 9 rac{16}{1^2} = 27 - 2 - 144 = 5.866
-
For :
y = 27 - 2(1.5) - 9 rac{16}{(1.5)^2} = 27 - 3 - 9 rac{16}{2.25} = 27 - 3 - 64 = 5.210
-
For :
y = 27 - 2(2) - 9 rac{16}{4} = 27 - 4 - 36 = -13 (evaluated incorrectly as positive initially)
-
For :
y = 27 - 2(2.5) - 9 rac{16}{(2.5)^2} = 27 - 5 - 9 rac{16}{6.25} = 27 - 5 - 23.04 = -1.21
-
For :
y = 27 - 2(3.5) - 9 rac{16}{(3.5)^2} = 27 - 7 - 9 rac{16}{12.25} = 27 - 7 - 11.72 = 8.28
-
For :
y = 27 - 2(4) - 9 rac{16}{16} = 27 - 8 - 9 = 10
Thus, the completed table looks like:
| x | 1 | 1.5 | 2 | 2.5 | 3.5 | 4 |
|---|---|---|---|---|---|---|
| y | 5.866 | 5.210 | -13 | -1.21 | 8.28 | 0 |
Step 2
Use the trapezium rule with all the values in the completed table to find an approximate value for the area of R, giving your answer to 2 decimal places.
Answer
The area can be approximated using the trapezium rule. The formula for the trapezium rule is given by:
Where is the width between the x-intervals. Here,
- For to , the intervals are 0.5 (since )
- The y-values from the table are used in the calculation:
Thus,
Calculating these values gives:
Thus, the approximate area of R is 11.42 (rounded to 2 decimal places).
Step 3
Use integration to find the exact value for the area of R.
Answer
To find the exact value of the area bounded by the curve and the x-axis, we can use integration:
We break this down into simpler parts:
-
Integrate :
-
Integrate :
-
Integrate :
Now substituting and solving gives:
Calculating at the limits:
- At :
- At :
Thus, the exact area:
Thus, the exact value for the area of R is 174.
