Photo AI
Figure 4 shows a closed letter box ABFEHGCD, which is made to be attached to a wall of a house - Edexcel - A-Level Maths Pure - Question 2 - 2014 - Paper 1
Question 2
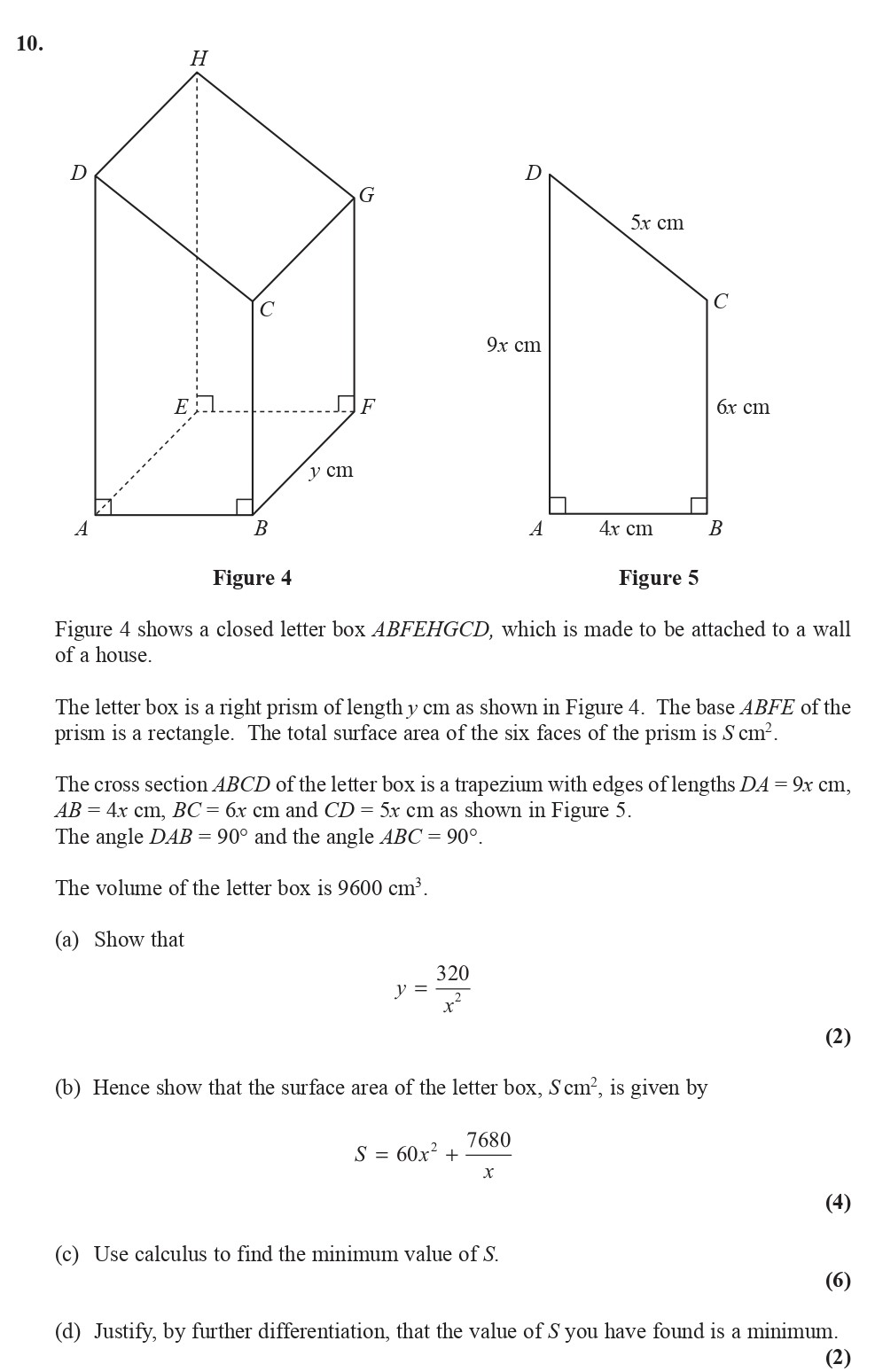
Figure 4 shows a closed letter box ABFEHGCD, which is made to be attached to a wall of a house. The letter box is a right prism of length y cm as shown in Figure 4.... show full transcript
Worked Solution & Example Answer:Figure 4 shows a closed letter box ABFEHGCD, which is made to be attached to a wall of a house - Edexcel - A-Level Maths Pure - Question 2 - 2014 - Paper 1
Step 1
Show that $y = \frac{320}{x^2}$
Answer
To show this, we start with the formula for the volume of a prism:
Here, the base ABCD is a trapezium given by the length of the parallel sides (AB and CD) and the height (BC):
Thus, the volume of the letter box can be expressed as:
From this, we can isolate y:
Step 2
Hence show that the surface area of the letter box, S cm², is given by $S = 60x + 7680 \div x$
Answer
The total surface area S of a prism can be calculated using the areas of the two bases along with the area of the side walls:
The lateral area can be obtained from the perimeter of the base multiplied by the height (length of the prism, y):
So:
Therefore, substituting y into the surface area equation:
After simplifying:
Step 3
Use calculus to find the minimum value of S.
Answer
To find the minimum value of S, we first differentiate S with respect to x:
Setting the derivative equal to zero to find critical points:
This gives:
Solving for x:
To verify it's a minimum, we can check the second derivative:
Since S'' is positive when x > 0, S has a local minimum at this point.
Step 4
Justify, by further differentiation, that the value of S you have found is a minimum.
Answer
Taking the second derivative confirmed that:
for all x > 0. Since the second derivative is positive, the function S is concave up at the point x = 8, confirming that this is indeed a minimum value for S.
