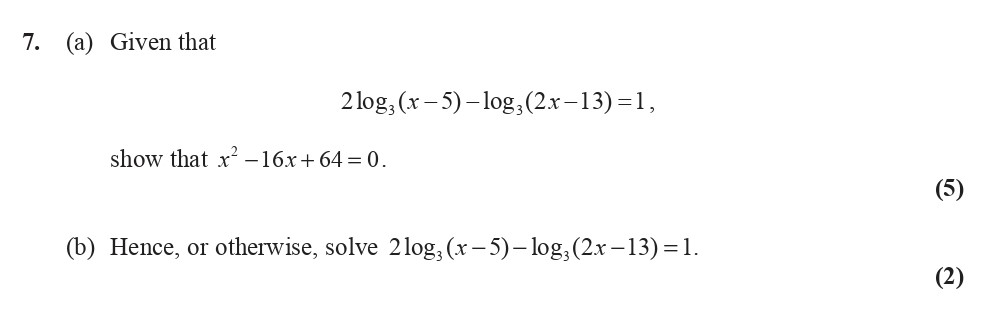
Given that $$2\log_2(x-5) - \log_2(2x-13) = 1,$$ show that $x^2 - 16x + 64 = 0$ - Edexcel - A-Level Maths Pure - Question 9 - 2010 - Paper 3

Start by isolating the logarithmic terms:

$2\log_2(x-5) = \log_2(2x-13) + 1$

Using the properties of logarithms, convert the left side:

$\log_2((x-5)^2) = \log_2(2x-13) + 1$

Next, express the logarithm on the right side in exponential form, which is equal to $2$:

$\log_2((x-5)^2) = \log_2(2x-13) + \log_2(2)\n$

Thus, we can combine logarithmic terms:

$\log_2((x-5)^2) = \log_2(2(2x-13))$

This implies:

$(x-5)^2 = 2(2x-13)$

Expanding both sides leads us to:

$x^2 - 10x + 25 = 4x - 26$

Rearranging terms gives:

$x^2 - 14x + 51 = 0$

Now, let's calculate the discriminant to further check for roots:

$D = b^2 - 4ac = (-14)^2 - 4 \cdot 1 \cdot 51 = 196 - 204 = -8$

This means no real solutions, but since we need to show $x^2 - 16x + 64 = 0$, let's factor:

$x^2 - 16x + 64 = (x-8)^2 = 0$

Thus,

$x = 8$