Photo AI
Figure 2 shows a sketch of part of the curve C with equation $y = x \ln x, \, x > 0$ The line I is the normal to C at the point $P(e, e)$ - Edexcel - A-Level Maths Pure - Question 3 - 2018 - Paper 2
Question 3
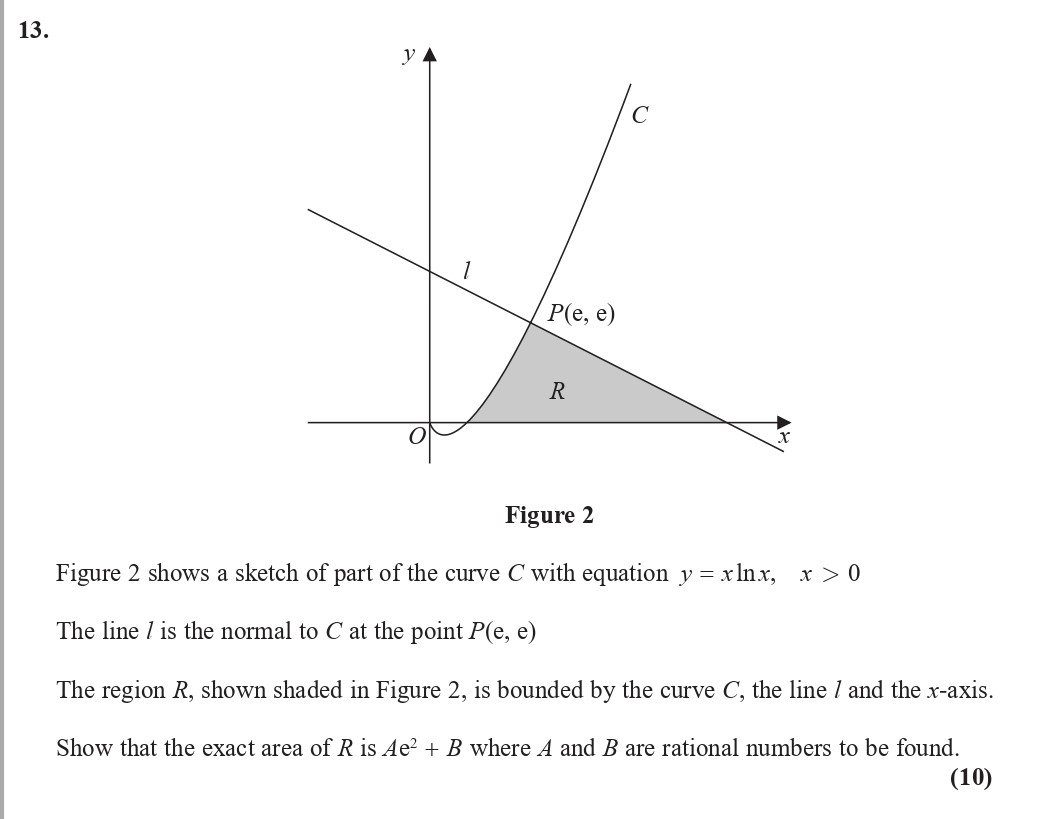
Figure 2 shows a sketch of part of the curve C with equation $y = x \ln x, \, x > 0$ The line I is the normal to C at the point $P(e, e)$. The region R, shown shad... show full transcript
Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve C with equation $y = x \ln x, \, x > 0$ The line I is the normal to C at the point $P(e, e)$ - Edexcel - A-Level Maths Pure - Question 3 - 2018 - Paper 2
Step 1
Show that the exact area of R is $Ae^2 + B$
Answer
To determine the area of region R, we begin by identifying the relevant boundaries. The area under the curve can be assessed using integration.
-
Determine the area bounded by curve C and the x-axis:
- The equation of the curve is given as .
- Find the area from to :
Using integration by parts, let:
- Therefore, and .
By applying integration by parts:
- Evaluating the definite integral gives:
Therefore, the area between the curve and the x-axis from to is:
-
Include the area under the line I:
- The line I is the normal to the curve at point ,
- The slope of the curve at this point is given by:
- Thus, the slope of the normal is .
- The equation of the normal line is thus:
-
Final Area Calculation:
- We then compute the area between and beneath line I,
- This evaluates to:
- Bringing it all together yields:
Thus, the area can be expressed as: where , and is the rational number corresponding to the non- term.
