Photo AI
Figure 2 shows a sketch of the curve C with equation $y = f(x)$ where $f(x) = 4( x^2 - 2)e^{-2x}$, $x \in \mathbb{R}$ (a) Show that $f'(x) = 8(2 + x - x^2)e^{-2x}$ - Edexcel - A-Level Maths Pure - Question 9 - 2020 - Paper 1
Question 9
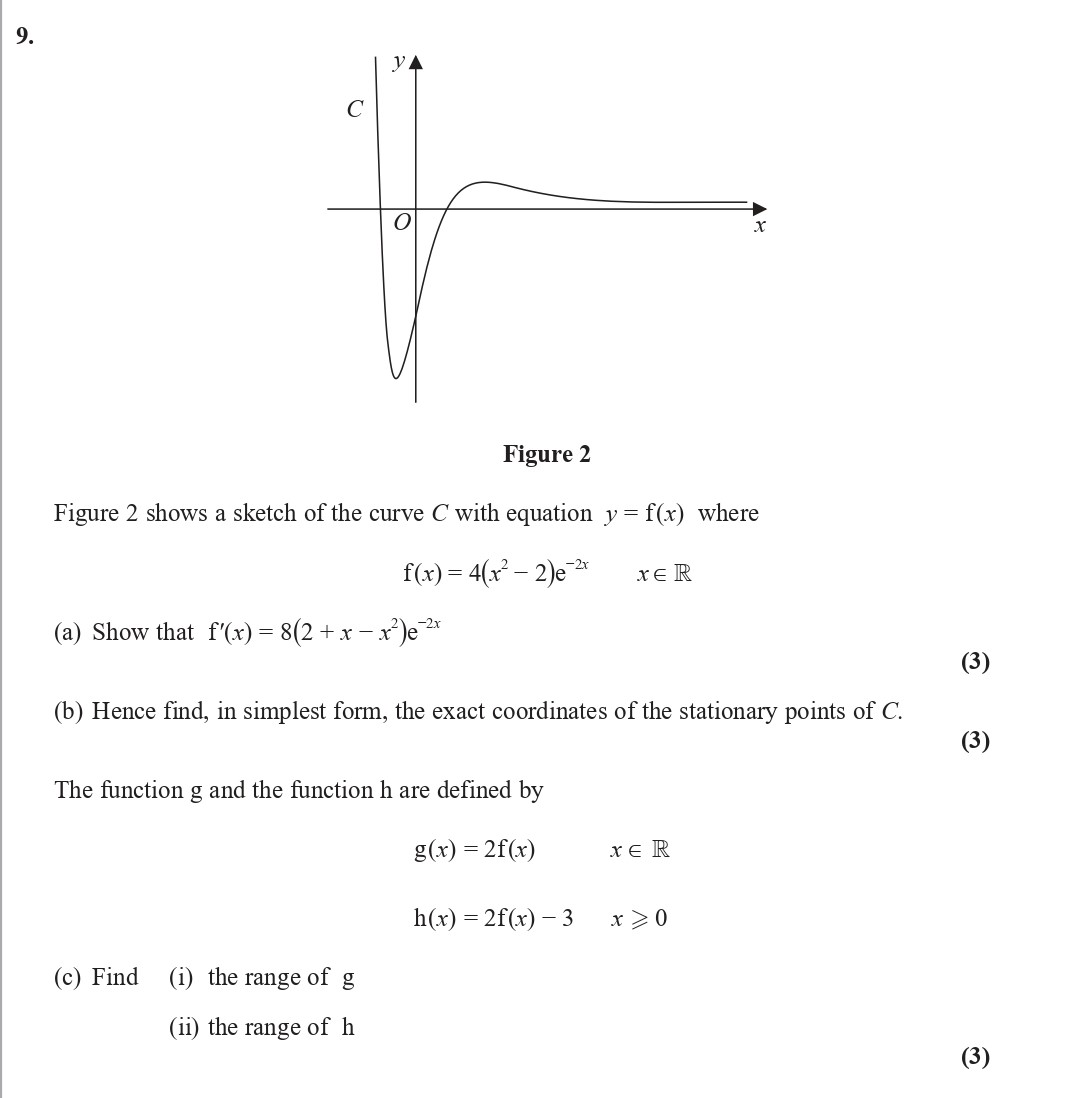
Figure 2 shows a sketch of the curve C with equation $y = f(x)$ where $f(x) = 4( x^2 - 2)e^{-2x}$, $x \in \mathbb{R}$ (a) Show that $f'(x) = 8(2 + x - x^2)e^{-2x}$.... show full transcript
Worked Solution & Example Answer:Figure 2 shows a sketch of the curve C with equation $y = f(x)$ where $f(x) = 4( x^2 - 2)e^{-2x}$, $x \in \mathbb{R}$ (a) Show that $f'(x) = 8(2 + x - x^2)e^{-2x}$ - Edexcel - A-Level Maths Pure - Question 9 - 2020 - Paper 1
Step 1
Show that $f'(x) = 8(2 + x - x^2)e^{-2x}$
Answer
To differentiate the function , we will use the product rule, which states that if we have two functions and , then ( (uv)' = u'v + uv' ).
Let:
- , hence .
- , hence .
Now applying the product rule:
This simplifies as follows:
Combining terms, we get:
Thus, we have shown that .
Step 2
Hence find, in simplest form, the exact coordinates of the stationary points of C.
Answer
To find the stationary points of the curve, we set :
Since is never zero, we focus on:
Rearranging the equation leads to:
Factoring gives:
This results in:
To find the corresponding coordinates:
- For :
- For :
Thus, the stationary points are:
Step 3
Step 4
