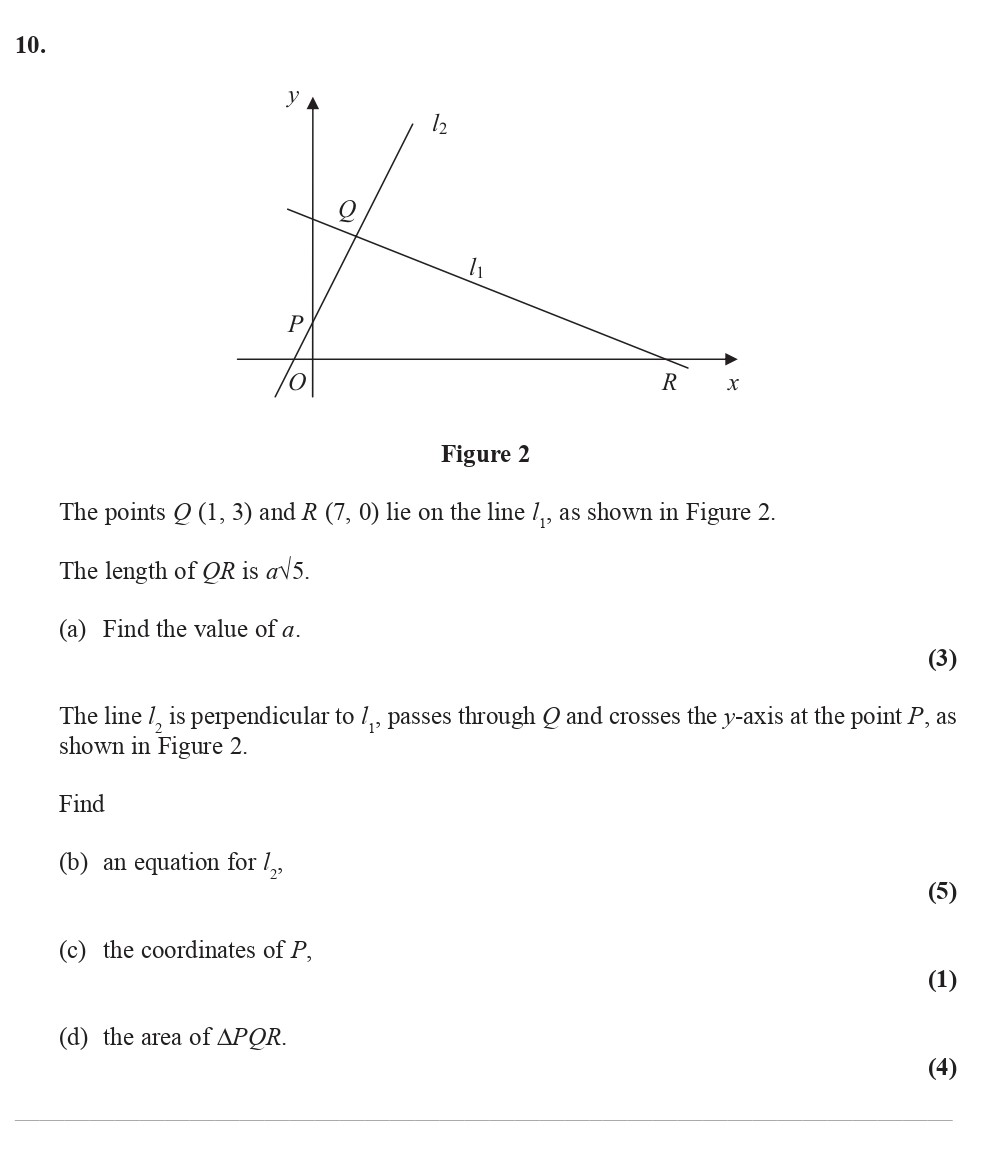
The points Q(1, 3) and R(7, 0) lie on the line l1, as shown in Figure 2 - Edexcel - A-Level Maths Pure - Question 3 - 2008 - Paper 1

Since l2 is perpendicular to l1, we first find the gradient of l1, which can be determined from the two points Q and R:

The slope (gradient) of QR is:

$m_{QR} = \frac{0 - 3}{7 - 1} = \frac{-3}{6} = -\frac{1}{2}$

The gradient of l2 (perpendicular) is the negative reciprocal:

$m_{l2} = 2$

Using point-slope form with point Q(1, 3):

$y - 3 = 2(x - 1)$

This simplifies to:

$y = 2x + 1$

To find the point P where l2 crosses the y-axis, we set x = 0 in the equation of l2:

$y = 2(0) + 1 = 1$

Thus, the coordinates of P are (0, 1).

To find the area of triangle PQR, we can use the formula for the area given vertices:

$\text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|$

Using Q(1, 3), R(7, 0), and P(0, 1), we have:

$\text{Area} = \frac{1}{2} \left| 1(0 - 1) + 7(1 - 3) + 0(3 - 0) \right|$

Calculating:

$= \frac{1}{2} \left| 1(-1) + 7(-2) + 0 \right| = \frac{1}{2} \left| -1 - 14 \right| = \frac{1}{2}(15) = 7.5$

Thus, the area of ΔPQR is 7.5.