Photo AI
A curve has parametric equations $x = an^2 t, \quad y = \\sin t, \quad 0 < t < \frac{\pi}{2}$ - Edexcel - A-Level Maths Pure - Question 7 - 2007 - Paper 8
Question 7
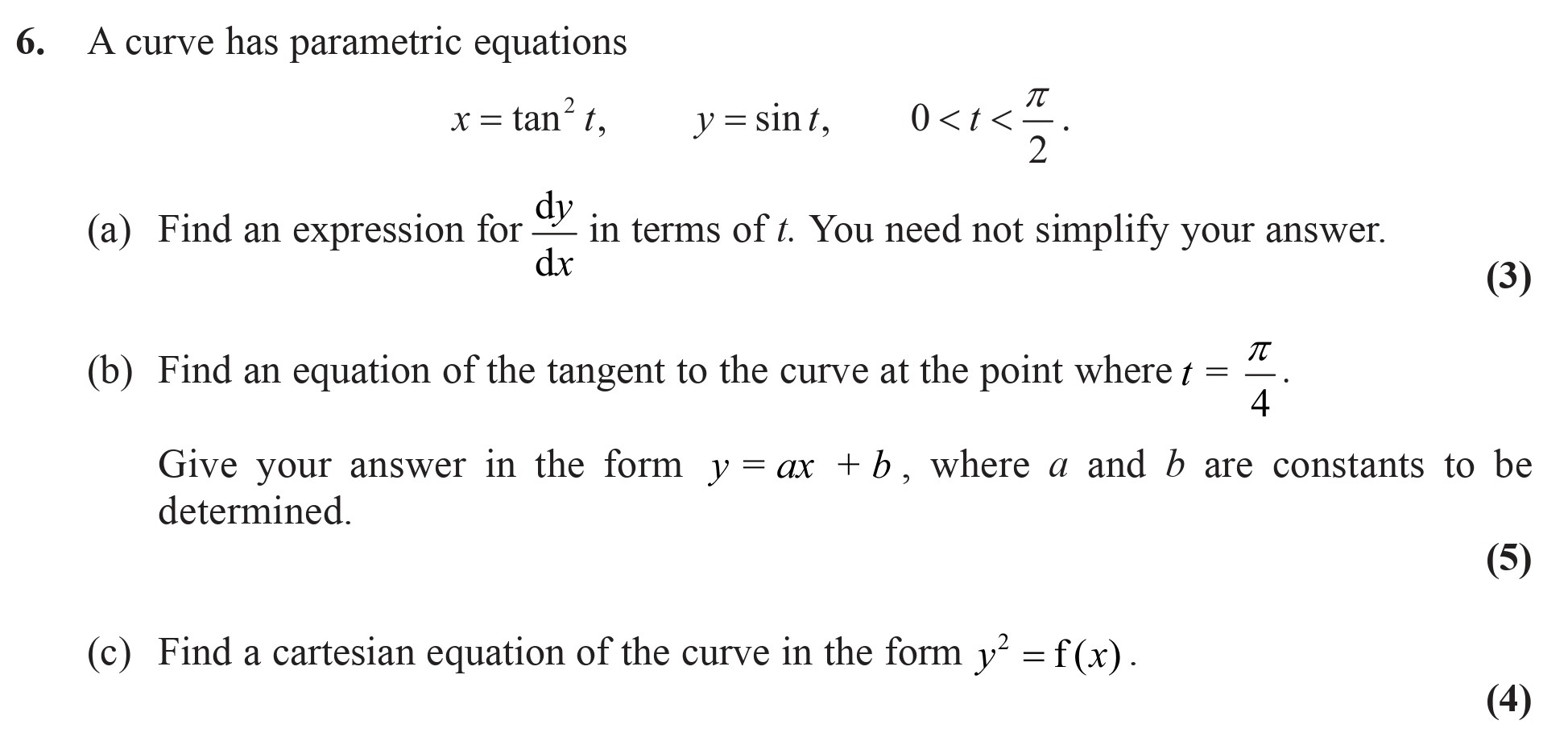
A curve has parametric equations $x = an^2 t, \quad y = \\sin t, \quad 0 < t < \frac{\pi}{2}$. (a) Find an expression for \(\frac{dy}{dx}\) in terms of \(t\). Y... show full transcript
Worked Solution & Example Answer:A curve has parametric equations $x = an^2 t, \quad y = \\sin t, \quad 0 < t < \frac{\pi}{2}$ - Edexcel - A-Level Maths Pure - Question 7 - 2007 - Paper 8
Step 1
Step 2
Find an equation of the tangent to the curve at the point where \(t = \frac{\pi}{4}\)
Answer
First, we find the coordinates of the point at (t = \frac{\pi}{4}):
- (x = \tan^2\left(\frac{\pi}{4}\right) = 1)
- (y = \sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2})
Now, we calculate (\frac{dy}{dx}) at this point:
- Using (t = \frac{\pi}{4}) in the expression:
Thus, the slope of the tangent line (m = \frac{1}{4}).
Using point-slope form, we have:
Simplifying gives:
Step 3
Find a cartesian equation of the curve in the form \(y^2 = f(x)\)
Answer
Starting from the parametric equations:
- We have (x = \tan^2 t) and (y = \sin t).
Using the Pythagorean identity:
Substituting (x = \tan^2 t) into the equation gives:
- Rearranging leads to:
Thus, the Cartesian equation is:
