Photo AI
8. (a) By writing sec θ = \frac{1}{cos θ}, show that \frac{d}{dθ}(sec θ) = sec θ tan θ (b) Given that \( x = e^{sec y} \), \( x > e, \; 0 < y < \frac{π}{2} \) show that \( \frac{dy}{dx} = \frac{1}{x g(x)} \), \; \( x > e \) where g(x) is a function of ln x. - Edexcel - A-Level Maths Pure - Question 8 - 2018 - Paper 5
Question 8
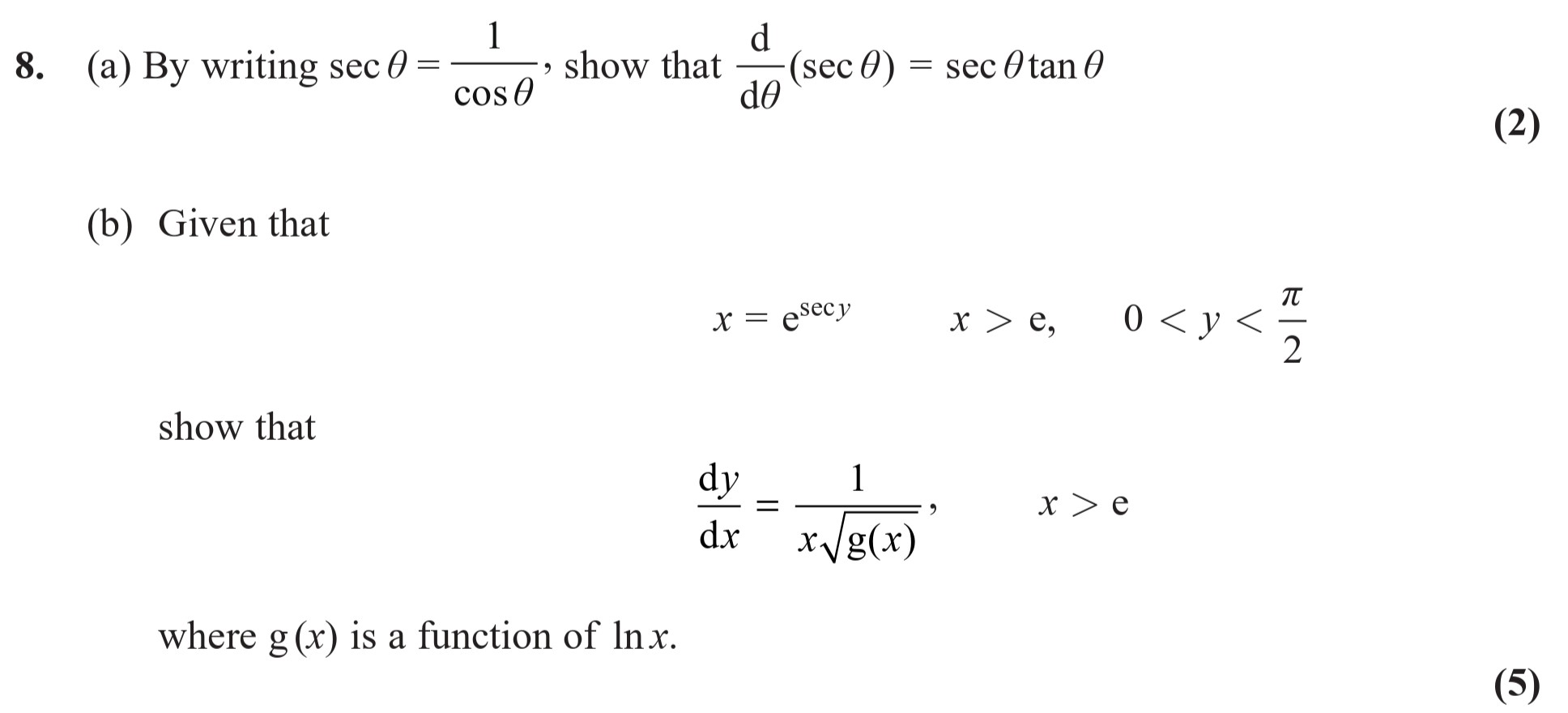
8. (a) By writing sec θ = \frac{1}{cos θ}, show that \frac{d}{dθ}(sec θ) = sec θ tan θ (b) Given that \( x = e^{sec y} \), \( x > e, \; 0 < y < \frac{π}{2} \) sho... show full transcript
Worked Solution & Example Answer:8. (a) By writing sec θ = \frac{1}{cos θ}, show that \frac{d}{dθ}(sec θ) = sec θ tan θ (b) Given that \( x = e^{sec y} \), \( x > e, \; 0 < y < \frac{π}{2} \) show that \( \frac{dy}{dx} = \frac{1}{x g(x)} \), \; \( x > e \) where g(x) is a function of ln x. - Edexcel - A-Level Maths Pure - Question 8 - 2018 - Paper 5
Step 1
By writing sec θ = \frac{1}{cos θ}, show that \frac{d}{dθ}(sec θ) = sec θ tan θ
Answer
To find ( \frac{d}{dθ}(sec θ) ), we can express sec θ as ( \frac{1}{cos θ} ).
Utilizing the chain rule:
We know ( \frac{d}{dθ}(cos θ) = -sin θ ), so:
Thus, we have shown that ( \frac{d}{dθ}(sec θ) = sec θ tan θ ).
Step 2
Given that \( x = e^{sec y} \), \; x > e, \; 0 < y < \frac{π}{2} \) show that \( \frac{dy}{dx} = \frac{1}{x g(x)} \), \; \( x > e \)
Answer
Starting from the equation ( x = e^{sec y} ), we differentiate both sides with respect to x:
( \frac{dx}{dy} = e^{sec y} sec y tan y )
Now we rearrange for ( \frac{dy}{dx} ):
Next, we rewrite ( e^{sec y} ) in terms of x:
Recognizing that the function g(x) relates to ln x, we can establish that:
Thus, we have confirmed ( \frac{dy}{dx} = \frac{1}{x g(x)} ), where g(x) is a function of ln x.
