Figure 1 shows a plot of part of the curve with equation $y = \cos x$ where $x$ is measured in radians. Diagram 1, on the opposite page, is a copy of Figure 1. (a) Use Diagram 1 to show why the equation $$\cos x - 2x - \frac{1}{2} = 0$$ has only one real root, giving a reason for your answer. Given that the root of the equation is $\alpha$, and that $\alpha$ is small, (b) use the small angle approximation for $\cos x$ to estimate the value of $\alpha$ to 3 decimal places.

A-Level Edexcel Maths Pure Inequalities: Figure 1 shows a plot of part of

Figure 1 shows a plot of part of the curve with equation $y = \cos x$ where $x$ is measured in radians - Edexcel - A-Level Maths Pure - Question 3 - 2019 - Paper 1

Question 3

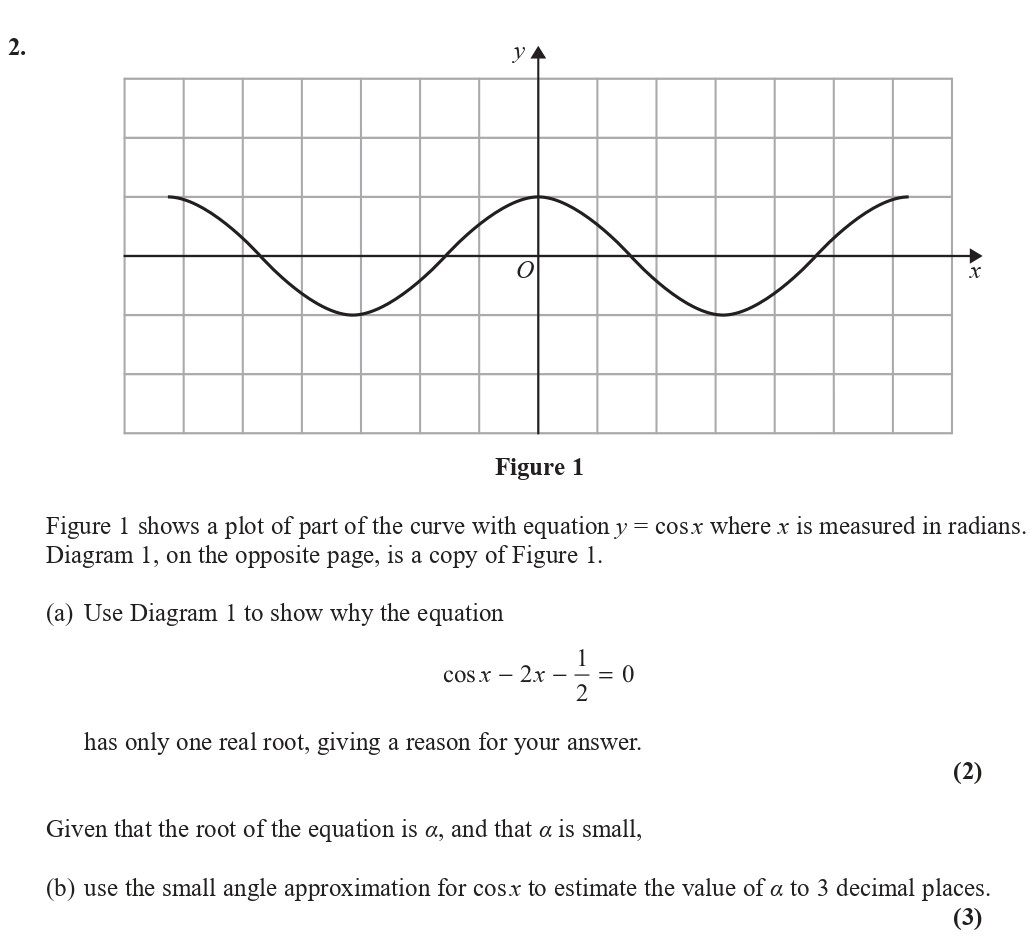
$Figure-1-shows-a-plot-of-part-of-the-curve-with-equation-$y-=-\cos-x$-where-$x$-is-measured-in-radians-Edexcel-A-Level Maths Pure-Question 3-2019-Paper 1.png$

Figure 1 shows a plot of part of the curve with equation $y = \cos x$ where $x$ is measured in radians. Diagram 1, on the opposite page, is a copy of Figure 1. (a) ... show full transcript

Worked Solution & Example Answer:Figure 1 shows a plot of part of the curve with equation $y = \cos x$ where $x$ is measured in radians - Edexcel - A-Level Maths Pure - Question 3 - 2019 - Paper 1

Step 1

Use Diagram 1 to show why the equation $\cos x - 2x - \frac{1}{2} = 0$ has only one real root

96%

114 rated

Answer

To demonstrate that the equation has only one real root, we need to analyze the graphs of both $y = \cos x$ and $y = 2x + \frac{1}{2}$ .

Graphing: The plot of $y = \cos x$ oscillates between -1 and 1 while $y = 2x + \frac{1}{2}$ is a straight line with a gradient of 2, crossing the y-axis at $\frac{1}{2}$ .
Analyzing Intersections: From Diagram 1, it is visible that the oscillating curve intersects the linear graph only once, particularly in the given range.
Explanatory Note: This indicates that the two functions have one intersection point, confirming that there is only one real solution to the equation. The increasing nature of the linear function ensures that it cannot cross the cosine curve again within the observed range.

Step 2

Use the small angle approximation for $\cos x$ to estimate the value of $\alpha$

99%

104 rated

Answer

Using the small angle approximation, we know that:

$\cos x \approx 1 - \frac{x^2}{2}$

Substituting this into the equation:

$1 - \frac{x^2}{2} - 2x - \frac{1}{2} = 0$

This simplifies to:

$-\frac{x^2}{2} - 2x + \frac{1}{2} = 0$

Multiplying through by -2 gives:

$x^2 + 4x - 1 = 0$

Next, we apply the quadratic formula:

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-4 \pm \sqrt{16 + 4}}{2} = \frac{-4 \pm \sqrt{20}}{2} = -2 \pm \sqrt{5}$

Choosing the negative root (since $\alpha$ is small), we have:

$\alpha = -2 + \sqrt{5}$

Calculating $\sqrt{5} \approx 2.236$ , therefore:

$\alpha \approx -2 + 2.236 = 0.236$

Hence, we conclude:

$\alpha \approx 0.236$

to three decimal places.

Figure 1 shows a plot of part of the curve with equation $y = \cos x$ where $x$ is measured in radians - Edexcel - A-Level Maths Pure - Question 3 - 2019 - Paper 1

Worked Solution & Example Answer:Figure 1 shows a plot of part of the curve with equation $y = \cos x$ where $x$ is measured in radians - Edexcel - A-Level Maths Pure - Question 3 - 2019 - Paper 1

Use Diagram 1 to show why the equation $\cos x - 2x - \frac{1}{2} = 0$ has only one real root

Use the small angle approximation for $\cos x$ to estimate the value of $\alpha$

Join the A-Level students using SimpleStudy...