Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$. The region $R_1$, shown shaded in Figure 2 is bounded by the curve and the negative x-axis. (a) Show that the exact area of $R_1$ is $\frac{20}{3}$. The region $R_2$, also shown shaded in Figure 2 is bounded by the curve, the positive x-axis and the line with equation $y = b$, where b is a positive constant and $0 < b < 4$. Given that the area of $R_1$ is equal to the area of $R_2$. (b) verify that $b$ satisfies the equation $(b + 2)^2(3b^2 - 20b + 20) = 0$. (c) Explain, with the aid of a diagram, the significance of the root 5.442.

Photo AI

Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 11 - 2019 - Paper 2

Question 11

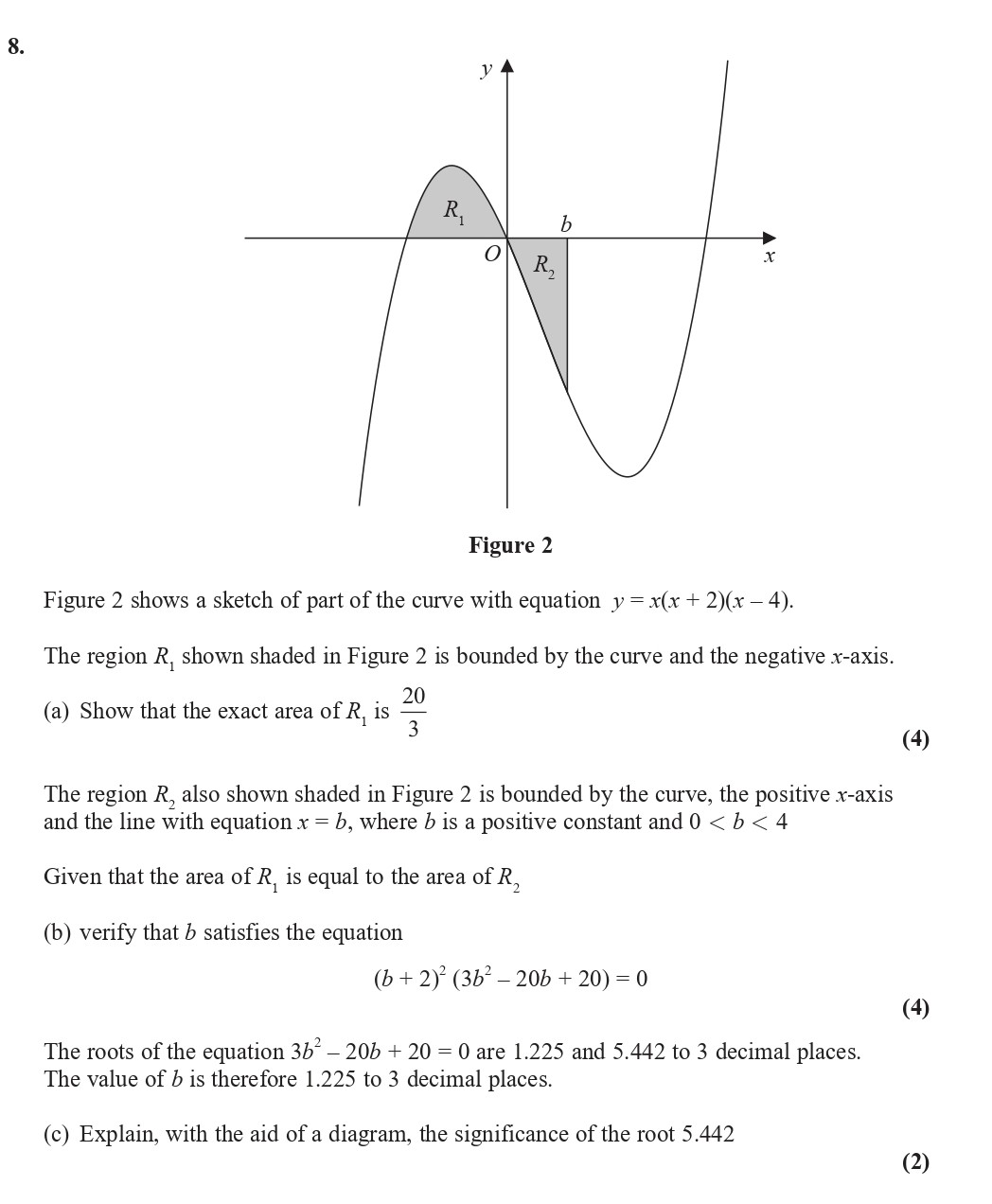
Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$. The region $R_1$, shown shaded in Figure 2 is bounded by the curve and the negat... show full transcript

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 11 - 2019 - Paper 2

Step 1

Show that the exact area of $R_1$ is $\frac{20}{3}$

96%

114 rated

Answer

To find the area of the region $R_1$ , we must evaluate the definite integral of the function from its intersection points with the x-axis. First, we expand the curve:

$y = x(x + 2)(x - 4) = x^3 - 2x^2 - 8x$

The area can be computed using the integral:

$A = -\int_{-2}^{0} (x^3 - 2x^2 - 8x) \, dx$

Calculating the integral:

Find the antiderivative:

$A = - \left[ \frac{1}{4} x^4 - \frac{2}{3} x^3 - 4 x^2 \right]_{-2}^{0}$
Evaluate at the limits:

$= - \left( 0 - \left( \frac{1}{4}(-2)^4 - \frac{2}{3}(-2)^3 - 4(-2)^2 \right) \right)$ $= - \left( 0 - \left( \frac{1}{4} \cdot 16 + \frac{16}{3} - 16 \right) \right)$

$= 20/3$

Step 2

verify that $b$ satisfies the equation $(b + 2)^2(3b^2 - 20b + 20) = 0$

99%

104 rated

Answer

To verify that $b$ satisfies the equation, we know from part (a) that the area of $R_1$ is $\frac{20}{3}$ . Since the area of $R_2$ is equal to the area of $R_1$ , we have:

$\int_{0}^{b} (x(x + 2)(x - 4)) \, dx = \frac{20}{3}$

This leads to:

Set up the equation:

$3b^2 - 20b + 20 = 0$
Factor the quadratic equation:

$\Rightarrow (b + 2)^2(3b^2 - 20b + 20) = 0$

Thus, we check that this verifies correctly, ensuring that $b = 2$ or the roots of the quadratic equation contribute to $R_2$ .

Step 3

Explain, with the aid of a diagram, the significance of the root 5.442

96%

101 rated

Answer

The root $5.442$ in the polynomial equation represents a point where the area described between the curve and the x-axis up to this point reflects a distinctive area structure. In the context of the graph, it indicates that at $x = 5.442$ , the area under the curve changes significantly, giving it a distinct value.

Create a diagram that shows the curve from $x = 0$ to $x = 6$ .
Shade the area between the curve and the x-axis to illustrate regions $R_1$ and $R_2$ .
Highlight the point $x = 5.442$ on the diagram to visualize where this area lies, emphasizing how it influences the total area calculation.

Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 11 - 2019 - Paper 2

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 11 - 2019 - Paper 2

Show that the exact area of $R_1$ is $\frac{20}{3}$

verify that $b$ satisfies the equation $(b + 2)^2(3b^2 - 20b + 20) = 0$

Explain, with the aid of a diagram, the significance of the root 5.442

Join the A-Level students using SimpleStudy...