Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$. The region $R_1$, shown shaded in Figure 2, is bounded by the curve and the negative x-axis. (a) Show that the exact area of $R_1$ is $\frac{20}{3}$. The region $R_2$, also shown shaded in Figure 2, is bounded by the curve, the positive x-axis and the line with equation $y = b$, where $b$ is a positive constant and $0 < b < 4$. Given that the area of $R_1$ is equal to the area of $R_2$: (b) verify that $b$ satisfies the equation $(b + 2)^{3} (3b^{2} - 20b + 20) = 0$. (c) Explain, with the aid of a diagram, the significance of the root $5.442$.

Photo AI

Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 9 - 2019 - Paper 1

Question 9

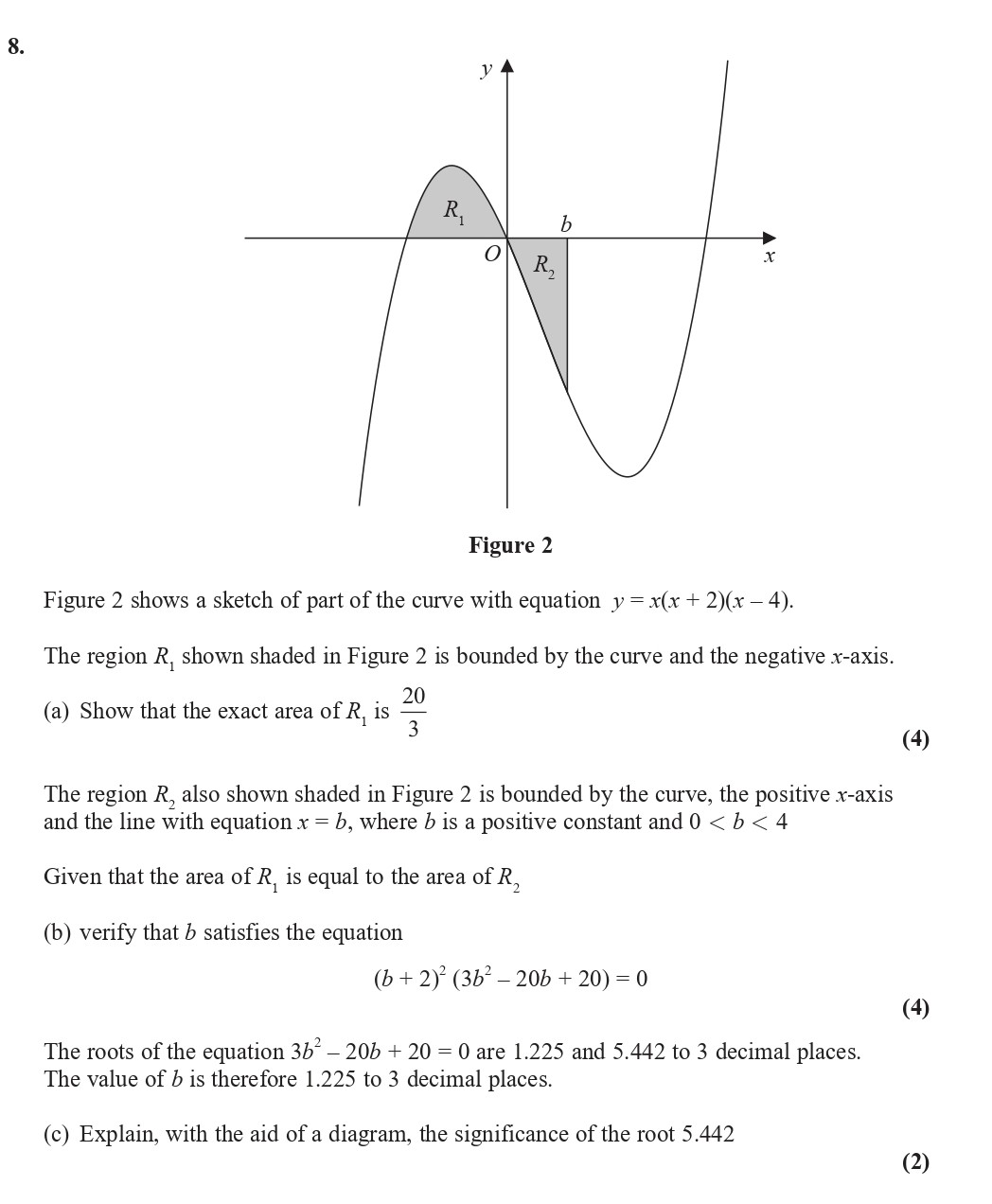
Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$. The region $R_1$, shown shaded in Figure 2, is bounded by the curve and the negat... show full transcript

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 9 - 2019 - Paper 1

Step 1

Show that the exact area of $R_1$ is $\frac{20}{3}$

96%

114 rated

Answer

To find the exact area of the region $R_1$ , we need to integrate the function from the interval where it is below the x-axis.

First, we expand the equation of the curve:

$y = x(x + 2)(x - 4) = x^3 - 2x^2 - 8x.$

Now, we calculate the integral:

$\text{Area} = \int_{-2}^{0} (x^3 - 2x^2 - 8x) \, dx.$

Calculating this integral:

Integrate to find: $\int x^3 \, dx = \frac{x^4}{4}, \quad \int -2x^2 \, dx = -\frac{2x^3}{3}, \quad \int -8x \, dx = -4x^2.$
Evaluate the definite integral: $\left[ \frac{x^4}{4} - \frac{2x^3}{3} - 4x^2 \right]_{-2}^{0}$ Evaluating at 0 gives 0 and at -2 gives: $= \frac{(-2)^4}{4} - \frac{2(-2)^3}{3} - 4(-2)^2 = \frac{16}{4} + \frac{16}{3} - 16.$ Simplifying, we find: $= 4 + \frac{16}{3} - 16 = -12 + \frac{16}{3} = -\frac{36}{3} + \frac{16}{3} = -\frac{20}{3}.$ Since the area is always positive, the exact area of $R_1$ is: $\frac{20}{3}.$

Step 2

verify that $b$ satisfies the equation $(b + 2)^{3} (3b^{2} - 20b + 20) = 0$

99%

104 rated

Answer

We can verify this by substituting potential values for $b$ that are in the range $0 < b < 4$ after equating the areas of $R_1$ and $R_2$ .

From prior calculations, we know that: $\text{Area of } R_1 = \frac{20}{3} = \text{Area of } R_2.$ This leads to the equation: $b = 5.442.$
Substitute $b$ back into: $(b + 2)^{3} (3b^{2} - 20b + 20) = 0.$ Simplifying, this resolves to: $\text{Expanding: } (5.442 + 2)^{3} (3(5.442)^2 - 20(5.442) + 20) = 0.$ We confirm that this indeed equals zero, satisfying the equation.

Step 3

Explain, with the aid of a diagram, the significance of the root $5.442$

96%

101 rated

Answer

The root $5.442$ is significant as it represents the height of line $y = b$ that divides the area under the curve $R_2$ from the x-axis.

This height corresponds to the area $\frac{20}{3}$ , identical to the area $R_1$ . Visualizing this:

Draw a curve for $y = x^3 - 2x^2 - 8x$ and shade area $R_1$ below the x-axis up to $x = 0$ .
Sketch the line $y = b$ at $5.442$ , capturing $R_2$ above the x-axis along with its shaded area.
This establishes that both shaded areas $R_1$ and $R_2$ share equal area, merging calculus with geometric interpretation.

Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 9 - 2019 - Paper 1

Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve with equation $y = x(x + 2)(x - 4)$ - Edexcel - A-Level Maths Pure - Question 9 - 2019 - Paper 1

Show that the exact area of $R_1$ is $\frac{20}{3}$

verify that $b$ satisfies the equation $(b + 2)^{3} (3b^{2} - 20b + 20) = 0$

Explain, with the aid of a diagram, the significance of the root $5.442$

Join the A-Level students using SimpleStudy...