Photo AI
1. (a) By writing sin 30° as sin (2θ + θ), show that sin 30° = 3sin θ – 4sin³θ - Edexcel - A-Level Maths Pure - Question 2 - 2007 - Paper 6
Question 2
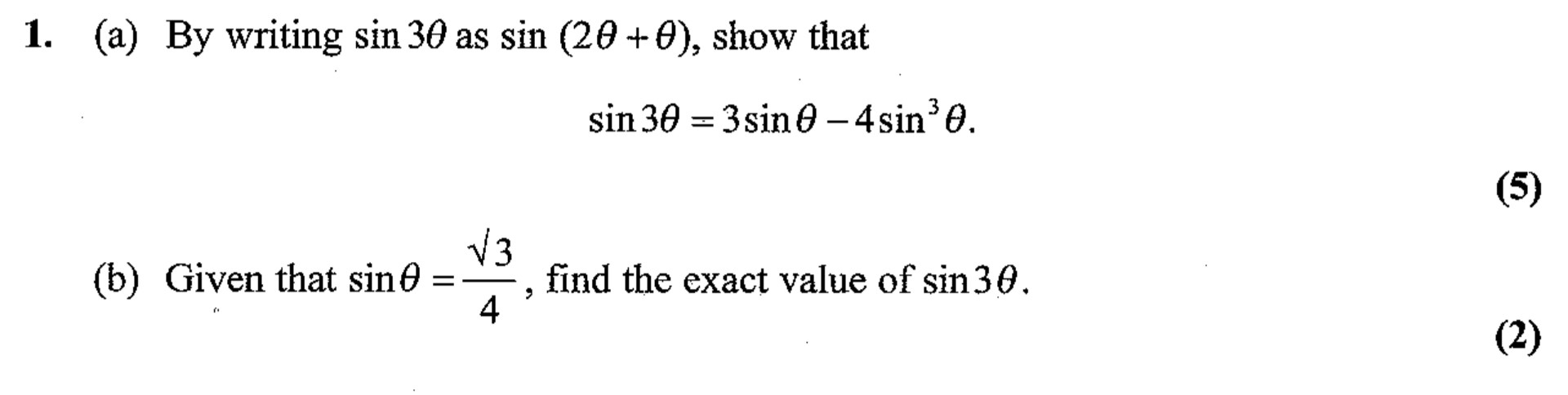
1. (a) By writing sin 30° as sin (2θ + θ), show that sin 30° = 3sin θ – 4sin³θ. (b) Given that sin θ = \( \frac{\sqrt{3}}{4} \), find the exact value of sin 30... show full transcript
Worked Solution & Example Answer:1. (a) By writing sin 30° as sin (2θ + θ), show that sin 30° = 3sin θ – 4sin³θ - Edexcel - A-Level Maths Pure - Question 2 - 2007 - Paper 6
Step 1
By writing sin 30° as sin (2θ + θ), show that
Answer
To show that , we start by expressing ( heta ) such that ( heta = 10° ). Therefore, we have:
Using the sine addition formula, we can state:
We know from trigonometric identities:
- ( \sin 2θ = 2\sin θ \cos θ )
- ( \cos 2θ = 1 - 2\sin²θ )
Substituting these identities, we get:
This simplifies to:
Factoring out ( \sin θ ):
Now by recognizing that ( 2\cos² θ + 1 - 2\sin² θ = 3 - 4\sin² θ ), we can rewrite it as:
Thus, we've shown the required expression.
Step 2
Given that sin θ = \( \frac{\sqrt{3}}{4} \), find the exact value of sin 30°.
Answer
Given that ( \sin θ = \frac{\sqrt{3}}{4} ), we substitute this value into the equation found in part (a):
Calculating each term:
First term:
Second term:
Now combining the two results:
Finding a common denominator (16):
Thus, the exact value of ( \sin 30° ) is:
\frac{9\sqrt{3}}{16} $$.