Photo AI
The curve C has the equation $$ ext{cos} 2x + ext{cos} 3y = 1, $$ $$ ewline -\frac{\pi}{4} \leq x \leq \frac{\pi}{4}, \quad 0 \leq y < \frac{\pi}{6} - Edexcel - A-Level Maths Pure - Question 5 - 2010 - Paper 7
Question 5
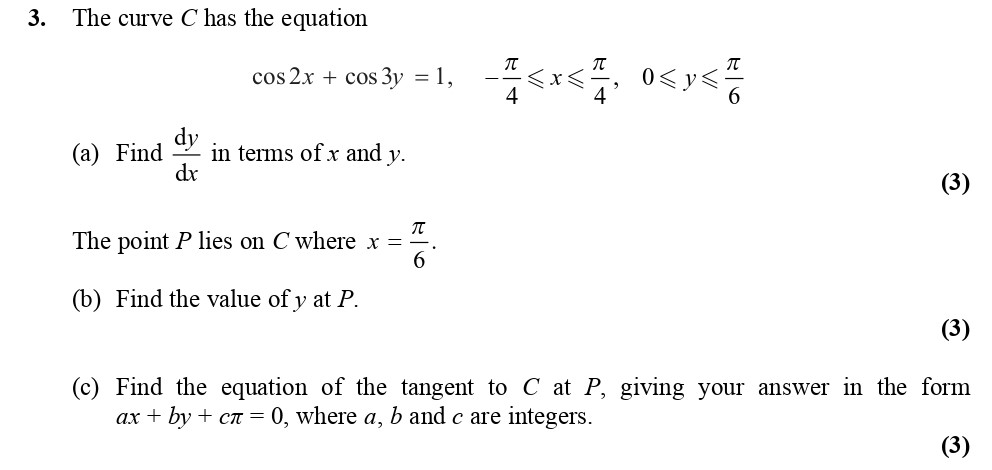
The curve C has the equation $$ ext{cos} 2x + ext{cos} 3y = 1, $$ $$ ewline -\frac{\pi}{4} \leq x \leq \frac{\pi}{4}, \quad 0 \leq y < \frac{\pi}{6}. $$ (a) Fin... show full transcript
Worked Solution & Example Answer:The curve C has the equation $$ ext{cos} 2x + ext{cos} 3y = 1, $$ $$ ewline -\frac{\pi}{4} \leq x \leq \frac{\pi}{4}, \quad 0 \leq y < \frac{\pi}{6} - Edexcel - A-Level Maths Pure - Question 5 - 2010 - Paper 7
Step 1
Find \(\frac{dy}{dx}\) in terms of x and y.
Answer
To find (\frac{dy}{dx}), we differentiate the equation (\text{cos} 2x + \text{cos} 3y = 1) implicitly with respect to x:
- Differentiate (\text{cos} 2x):
(\frac{d}{dx} \text{cos} 2x = -2\sin 2x) - Differentiate (\text{cos} 3y):
Using the chain rule, (\frac{d}{dx} \text{cos} 3y = -3\sin 3y \cdot \frac{dy}{dx}) - Set the derivative equal to 0:
[-2\sin 2x - 3\sin 3y \cdot \frac{dy}{dx} = 0] - Solve for (\frac{dy}{dx}):
[\frac{dy}{dx} = \frac{2\sin 2x}{3\sin 3y}]
Step 2
Find the value of y at P.
Answer
At the point (P), where (x = \frac{\pi}{6}):
- Substitute (x = \frac{\pi}{6}) into the original equation:
[\text{cos} \left(2 \cdot \frac{\pi}{6}\right) + \text{cos} 3y = 1]
[\text{cos} \left(\frac{\pi}{3}\right) + \text{cos} 3y = 1]
[\frac{1}{2} + \text{cos} 3y = 1] - Rearranging gives:
[\text{cos} 3y = 1 - \frac{1}{2} = \frac{1}{2}] - Therefore, (3y) can be calculated as follows:
[3y = \frac{\pi}{3} + 2k\pi \quad (k \in \mathbb{Z})] - This leads to:
[y = \frac{\pi}{9} + \frac{2k\pi}{3}]
Step 3
Find the equation of the tangent to C at P.
Answer
-
We already know that at (x = \frac{\pi}{6}), (y = \frac{\pi}{9}).
-
Evaluate (\frac{dy}{dx}) at this point:
[\frac{dy}{dx} = \frac{2\sin(\frac{\pi}{3})}{3\sin(\frac{\pi}{3})} = \frac{2}{3}] -
The slope (m = \frac{2}{3}).
-
Using point-slope form (y - y_1 = m(x - x_1)):
[y - \frac{\pi}{9} = \frac{2}{3}\left(x - \frac{\pi}{6}\right)] -
Rearranging gives:
[2x - 3y + \frac{\pi}{2} - \frac{\pi}{3} = 0] -
To express it in the required form:
[6x - 9y - \frac{\pi}{2} = 0]Multiplying through appropriately will provide integer coefficients. The equation is then stated as:
[6x + 9y - 2\pi = 0]This gives integers a, b, and c.
