Photo AI
Figure 2 shows a sketch of part of the curve C with equation $y = x ext{ln} x$, $x > 0$ - Edexcel - A-Level Maths Pure - Question 1 - 2018 - Paper 2
Question 1
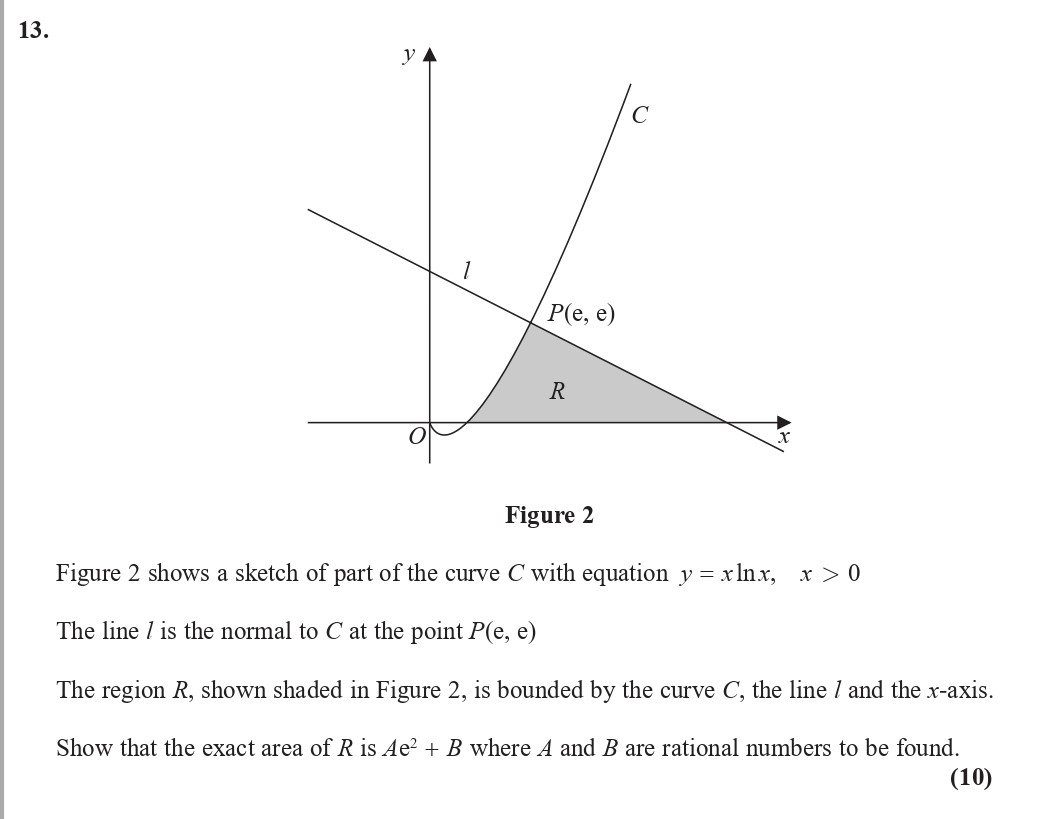
Figure 2 shows a sketch of part of the curve C with equation $y = x ext{ln} x$, $x > 0$. The line l is the normal to C at the point P(e, e) The region R, shown shad... show full transcript
Worked Solution & Example Answer:Figure 2 shows a sketch of part of the curve C with equation $y = x ext{ln} x$, $x > 0$ - Edexcel - A-Level Maths Pure - Question 1 - 2018 - Paper 2
Step 1
Finding the Area of R
Answer
To find the area of the region R, we need to integrate the function describing the curve from the appropriate limits.
Step 1: Identify the curve and limits
The curve is given by the equation: We will integrate this function between the x-values corresponding to the intersection points with the x-axis and the normal line.
Step 2: Determine intersection points
We find where the curve intersects the x-axis. Setting : This occurs at .
Step 3: Evaluate the normal line equation
At point P(e, e), the normal line must be calculated. The gradient of the curve C at is: rac{dy}{dx} = ext{ln} e + 1 = 2 Thus, the slope of the normal line, which is the negative reciprocal, is - rac{1}{2}. Now, using point-slope form to find the normal line: y - e = - rac{1}{2}(x - e) This simplifies to: y = - rac{1}{2}x + rac{e}{2} + e = - rac{1}{2}x + rac{3e}{2}
Step 4: Set up the integral
Now, we compute the area A: Thus:
Step 5: Perform the integration
Calculate:
Using integration by parts: Let and , then: du = rac{1}{x} \, dx \, , \quad v = rac{x^2}{2} This results in: ext{Area}_{ ext{curve}} = rac{e^2}{2} ext{ln} e - rac{1}{2} ext{Area}_{ ext{line}} After evaluating and simplifying, we find where A and B are rational numbers.
