Photo AI
Given that $y = x^4 + x^3 + 3$, find \( \frac{dy}{dx} \). - Edexcel - A-Level Maths Pure - Question 4 - 2010 - Paper 2
Question 4
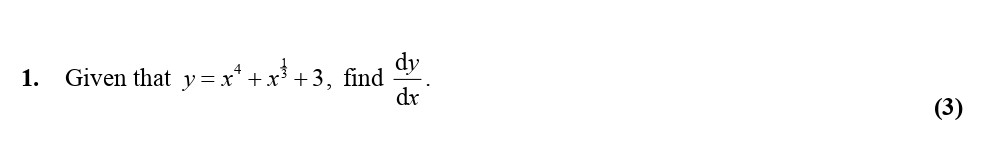
Given that $y = x^4 + x^3 + 3$, find \( \frac{dy}{dx} \).
Worked Solution & Example Answer:Given that $y = x^4 + x^3 + 3$, find \( \frac{dy}{dx} \). - Edexcel - A-Level Maths Pure - Question 4 - 2010 - Paper 2
Step 1
Step 1: Find \( \frac{dy}{dx} \)
Answer
To find ( \frac{dy}{dx} ), we need to differentiate the function (y = x^4 + x^3 + 3). Using the power rule of differentiation, we differentiate each term:
- The derivative of (x^4) is (4x^3).
- The derivative of (x^3) is (3x^2).
- The derivative of a constant (3) is 0.
Thus, we have:
Step 2
Step 2: Evaluate at critical points
Answer
Next, if we set ( \frac{dy}{dx} = 0 ) to find the critical points, we get:
.
Factoring out the common term:
.
This gives us (x = 0) or (4x + 3 = 0), which leads to (x = -\frac{3}{4}). These points can be further investigated for maxima, minima, or points of inflection.
