A-Level Edexcel Maths Pure Integration: Given that $$2 \, \log

Given that $$2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1,$$ show that $x^2 - 16x + 64 = 0.$ (b) Hence, or otherwise, solve $2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1.$ - Edexcel - A-Level Maths Pure - Question 8 - 2010 - Paper 3

Question 8

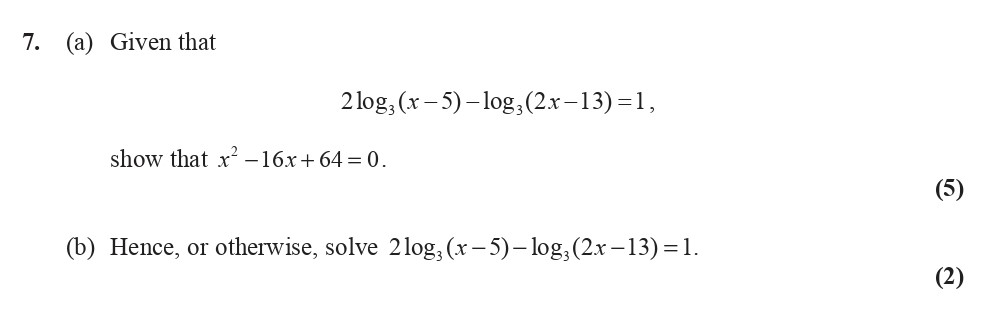
$Given-that--$$2-\,-\log_{10}-(x---5)---\log_{10}-(2x---13)-=-1,$$-show-that-$x^2---16x-+-64-=-0.$--(b)-Hence,-or-otherwise,-solve-$2-\,-\log_{10}-(x---5)---\log_{10}-(2x---13)-=-1.$-Edexcel-A-Level Maths Pure-Question 8-2010-Paper 3.png$

Given that $$2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1,$$ show that $x^2 - 16x + 64 = 0.$ (b) Hence, or otherwise, solve $2 \, \log_{10} (x - 5) - \log_{10}... show full transcript

Worked Solution & Example Answer:Given that $$2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1,$$ show that $x^2 - 16x + 64 = 0.$ (b) Hence, or otherwise, solve $2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1.$ - Edexcel - A-Level Maths Pure - Question 8 - 2010 - Paper 3

Step 1

Show that $x^2 - 16x + 64 = 0$

96%

114 rated

Answer

Starting with the equation:

$2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1,$

we can rewrite it as:

$\log_{10} ((x - 5)^2) - \log_{10} (2x - 13) = 1.$
Using the properties of logarithms, this simplifies to:

$\log_{10} \left( \frac{(x - 5)^2}{2x - 13} \right) = 1.$
Exponentiating both sides, we get:

$\frac{(x - 5)^2}{2x - 13} = 10.$
Multiplying through by $(2x - 13)$ gives:

$(x - 5)^2 = 10(2x - 13).$
Expanding both sides:

$(x^2 - 10x + 25) = 20x - 130.$
Rearranging terms leads to:

$x^2 - 30x + 155 = 0.$
Factoring this quadratic equation yields:

$(x - 8)(x - 8) = 0,$
which simplifies to:

$x^2 - 16x + 64 = 0.$
Thus, we have shown the required result.

Step 2

Hence, or otherwise, solve $2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1$

99%

104 rated

Answer

From the previous equation, we know:

$(x - 8)(x - 8) = 0.$
So, the solutions are:

$x = 8.$
We substitute $x = 8$ back into the original equation to verify:

$2 \, \log_{10} (8 - 5) - \log_{10} (2(8) - 13) = 1,$ which simplifies to:

$2 \, \log_{10} (3) - \log_{10} (3) = 1.$
This yields:

$\log_{10} (3) = 1,$
indicating our solution is valid. Therefore, the solution is:

$x = 8.$

Given that $$2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1,$$ show that $x^2 - 16x + 64 = 0.$ (b) Hence, or otherwise, solve $2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1.$ - Edexcel - A-Level Maths Pure - Question 8 - 2010 - Paper 3

Worked Solution & Example Answer:Given that $$2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1,$$ show that $x^2 - 16x + 64 = 0.$ (b) Hence, or otherwise, solve $2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1.$ - Edexcel - A-Level Maths Pure - Question 8 - 2010 - Paper 3

Show that $x^2 - 16x + 64 = 0$

Hence, or otherwise, solve $2 \, \log_{10} (x - 5) - \log_{10} (2x - 13) = 1$

Join the A-Level students using SimpleStudy...