Photo AI
Solve the simultaneous equations $$x - 2y = 1,$$ $$x^2 + y^2 = 29.$$ - Edexcel - A-Level Maths Pure - Question 7 - 2005 - Paper 1
Question 7
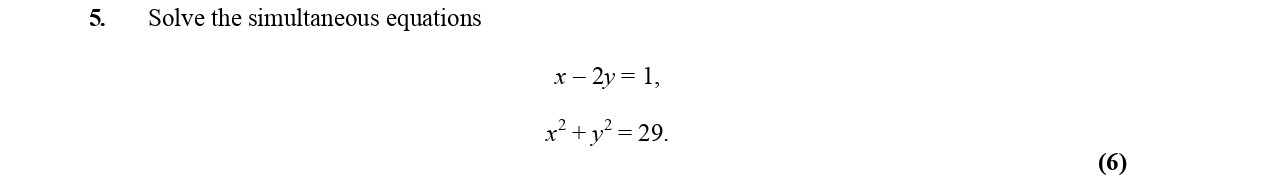
Solve the simultaneous equations $$x - 2y = 1,$$ $$x^2 + y^2 = 29.$$
Worked Solution & Example Answer:Solve the simultaneous equations $$x - 2y = 1,$$ $$x^2 + y^2 = 29.$$ - Edexcel - A-Level Maths Pure - Question 7 - 2005 - Paper 1
Step 1
Step 2
Step 3
Step 4
Step 6
