Photo AI
Figure 1 shows part of the curve with equation $y = \, \sqrt{\tan x}$ - Edexcel - A-Level Maths Pure - Question 8 - 2007 - Paper 8
Question 8
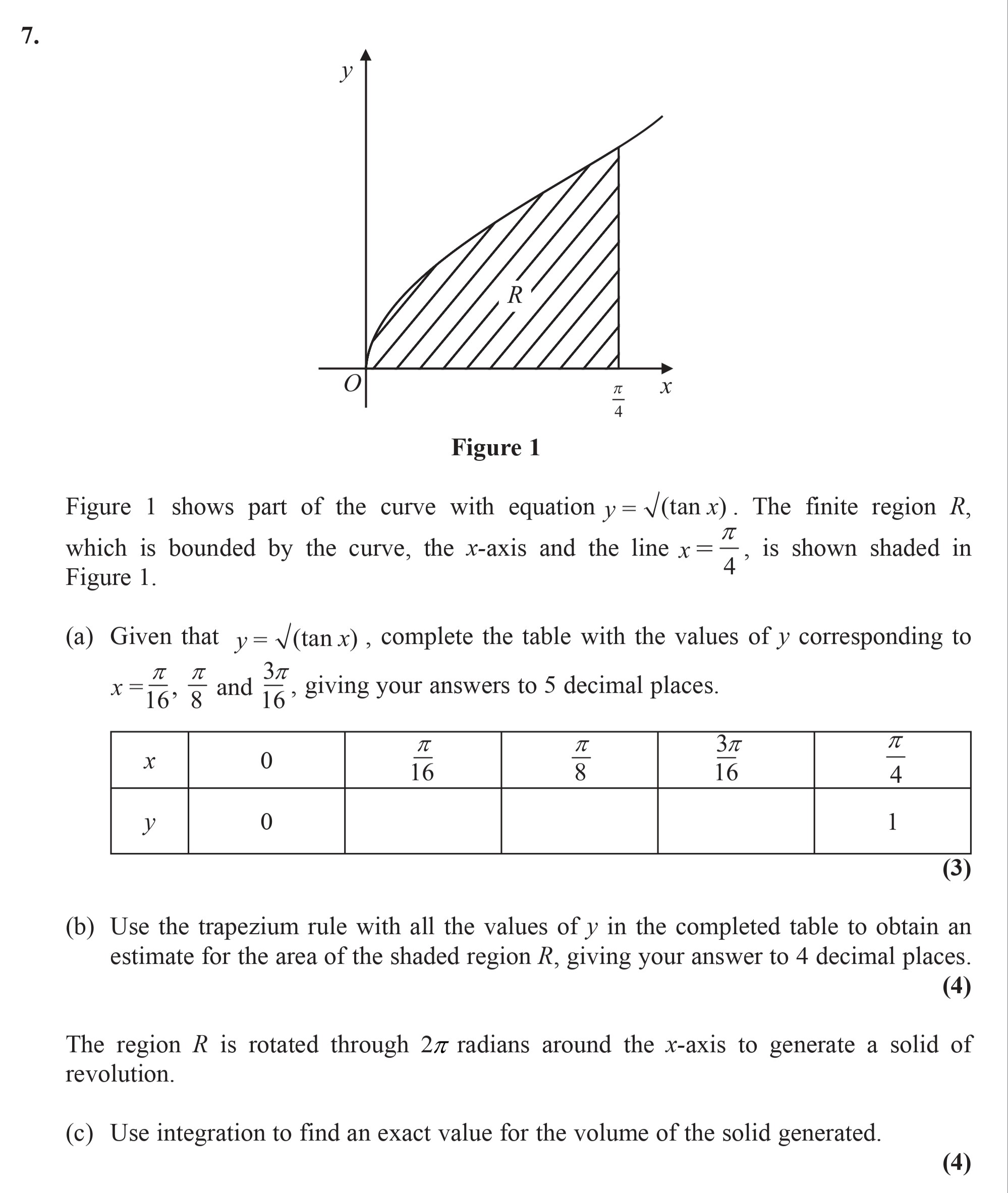
Figure 1 shows part of the curve with equation $y = \, \sqrt{\tan x}$. The finite region $R$, which is bounded by the curve, the x-axis and the line $x = \frac{\pi}{... show full transcript
Worked Solution & Example Answer:Figure 1 shows part of the curve with equation $y = \, \sqrt{\tan x}$ - Edexcel - A-Level Maths Pure - Question 8 - 2007 - Paper 8
Step 1
Step 2
Use the trapezium rule with all the values of $y$ in the completed table to obtain an estimate for the area of the shaded region $R$, giving your answer to 4 decimal places.
Answer
To apply the trapezium rule:
The formula is given by:
where:
Now substituting these values into the formula:
Calculating:
Thus, the estimated area of the shaded region is approximately: (to 4 decimal places).
Step 3
Use integration to find an exact value for the volume of the solid generated.
Answer
To find the volume of the solid generated by rotating the region about the x-axis, we use the formula for the volume of revolution:
Substituting gives:
This integral can be calculated as:
Calculating the limits:
-
At :
-
At :
Thus, combining these gives:
Therefore, the exact volume of the solid generated is:
