Photo AI
The curve C with equation $$y = \frac{p - 3x}{(2x - q)(x + 3)}$$ where p and q are constants, passes through the point \( \left( 3, \frac{1}{2} \right) \) and has two vertical asymptotes with equations \( x = 2 \) and \( x = -3 \) - Edexcel - A-Level Maths Pure - Question 14 - 2019 - Paper 2
Question 14
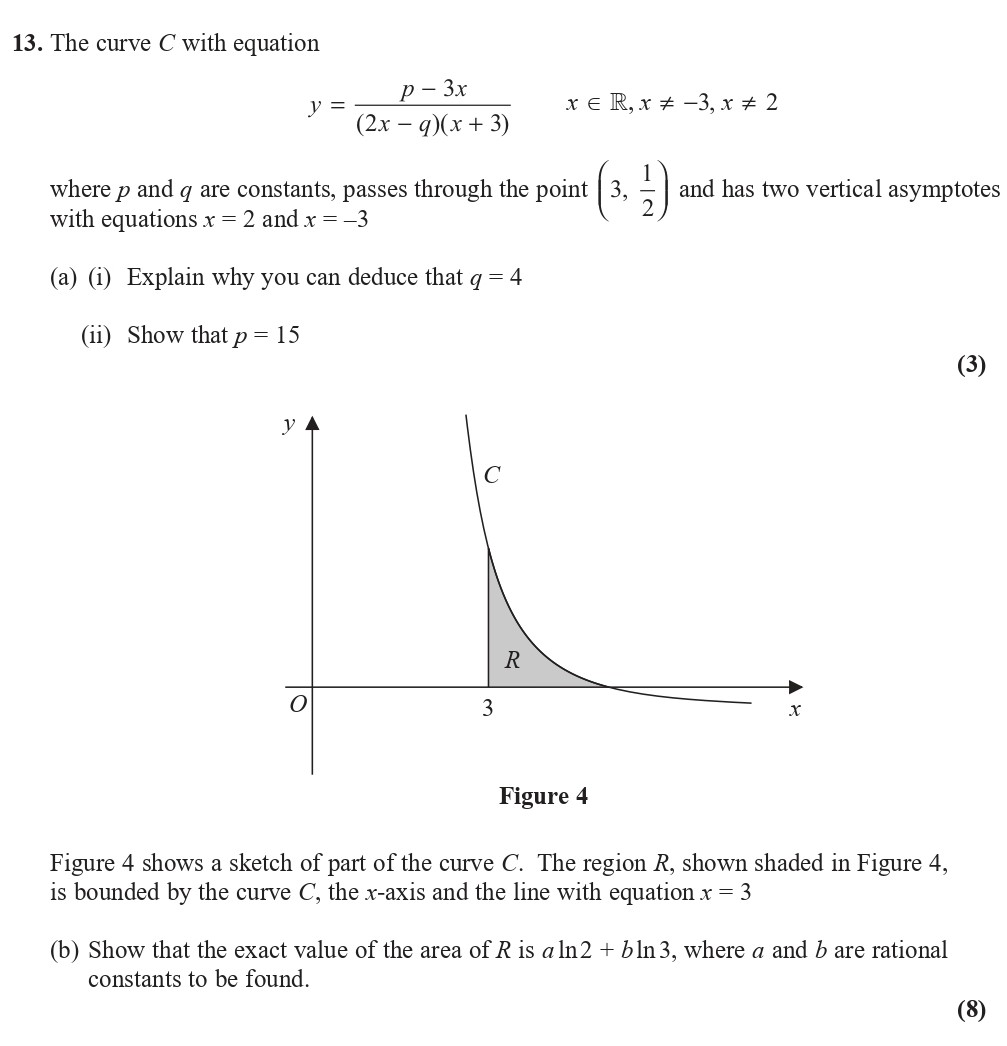
The curve C with equation $$y = \frac{p - 3x}{(2x - q)(x + 3)}$$ where p and q are constants, passes through the point \( \left( 3, \frac{1}{2} \right) \) and ha... show full transcript
Worked Solution & Example Answer:The curve C with equation $$y = \frac{p - 3x}{(2x - q)(x + 3)}$$ where p and q are constants, passes through the point \( \left( 3, \frac{1}{2} \right) \) and has two vertical asymptotes with equations \( x = 2 \) and \( x = -3 \) - Edexcel - A-Level Maths Pure - Question 14 - 2019 - Paper 2
Step 1
Explain why you can deduce q = 4
Answer
To deduce that ( q = 4 ), we note that the vertical asymptotes of the curve occur when the denominator equals zero. Given the equation of the curve, we have the terms ( 2x - q ) equating to zero at ( x = 2 ). Thus,
This explains why ( q ) must be equal to 4.
Step 2
Step 3
Show that the exact value of the area of R is a ln 2 + b ln 3
Answer
To determine the area of region R, we calculate:
.
Using partial fractions, we can express:
Finding A and B involves equating coefficients and matching terms. On solving, we get:
This allows us to integrate and find the area described by integrating from x=3 to x=5, yielding:
Calculating at the boundaries gives:
Thus, the exact value for the area of R is expressed as ( a \ln 2 + b \ln 3 ).
